Result Summary - Overall
Horizontal Brace Connection
Code=AISC 360-10 LRFD
 
Result Summary - Overall
geometries & weld limitations = PASS
limit states max ratio 
= 0.92
PASS
 
Right Brace - Brace to Gusset
geometries & weld limitations = PASS
limit states max ratio 
= 0.92
PASS
 
Right Brace - Gusset to Girder
geometries & weld limitations = PASS
limit states max ratio 
= 0.64
PASS
 
Right Brace - Gusset to Beam
geometries & weld limitations = PASS
limit states max ratio 
= 0.20
PASS

 
Left Brace - Brace to Gusset
geometries & weld limitations = PASS
limit states max ratio 
= 0.92
PASS
 
Left Brace - Gusset to Girder
geometries & weld limitations = PASS
limit states max ratio 
= 0.64
PASS
 
Left Brace - Gusset to Beam
geometries & weld limitations = PASS
limit states max ratio 
= 0.21
PASS

 
Beam to Girder
geometries & weld limitations = PASS
limit states max ratio 
= 0.47
PASS
 
 
Sketch
Horizontal Brace Connection
Code=AISC 360-10 LRFD
 
 
 
 
 
 
Members & Components Summary
Member
Brace Connection
Code=AISC 360-10 LRFD
 
Beam Section

W12X45
d
 = 12.100
[in]
bf
 = 8.050
[in]

tf
 = 0.575
[in]
tw
 = 0.335
[in]

kdes
 = 1.080
[in]
kdet
 = 1.375
[in]

k1
 = 0.938
[in]
A
 = 13.100
[in2]

 
Sx
 = 57.70
[in3]
Zx
 = 64.20
[in3]

 
Steel Grade A992
Fy
 = 50.0
[ksi]
Fu
 = 65.0
[ksi]

 
Column Section

W12X40
d
 = 11.900
[in]
bf
 = 8.010
[in]

tf
 = 0.515
[in]
tw
 = 0.295
[in]

kdes
 = 1.020
[in]
kdet
 = 1.375
[in]

k1
 = 0.875
[in]
A
 = 11.700
[in2]

 
Sx
 = 51.50
[in3]
Zx
 = 57.00
[in3]

 
Steel Grade A992
Fy
 = 50.0
[ksi]
Fu
 = 65.0
[ksi]

 
 
 
 
Gusset Plate Interface Forces Calculation
 

 
 

Brace Axial Force Load Case 1

 
Right and left brace force
R Prt
 = -35.00
[kips] (T)
L Plt
 = 35.00
[kips] (C)

Beam end shear & transfer force
Shear Rb
 = 25.00
[kips]
Transfer Ab
 = 15.00
[kips]

 
 

Top Brace Interface Forces

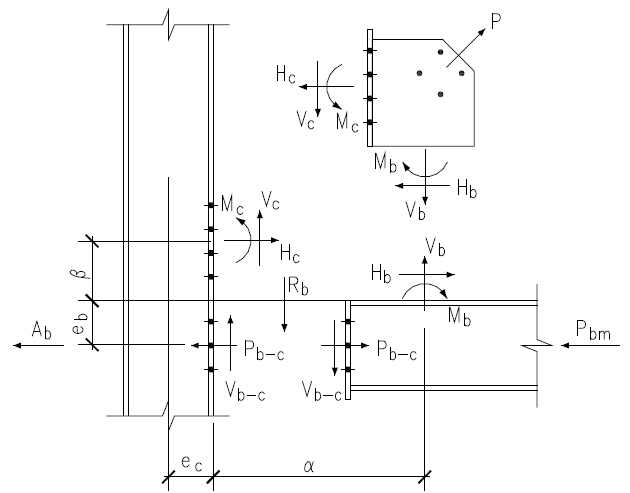
Refer to AISC 14th  Page 13-4 and Fig. 13-2 for all charts and definitions of variables and symbols shown in calculation below
eb
 = 0.168
[in]
ec
 = 0.148
[in]

α
 = 7.951
[in]
β
 = 6.983
[in]

θ
 = 45.0
[°]

K
 = eb tanθ - ec
 = 0.020
[in]
AISC 14th  Eq. 13-16
D
 = tan2 θ + (
α/β
)2
 = 2.297
AISC 14th  Eq. 13-24
K'
 = α ( tan θ +
α/β
)
 = 17.005
AISC 14th  Eq. 13-23
α
 = [ K' tan θ + K (
α/β
)2 ] / D
 = 7.003
[in]
AISC 14th  Eq. 13-21
β
 = ( K' - K tan θ ) / D
 = 6.983
[in]
AISC 14th  Eq. 13-22
r
 = [ ( eb + β ) 2 + ( ec + α ) 2 ]0.5
 = 10.112
[in]
AISC 14th  Eq. 13-6

Brace axial force
Pu
 = from user input
 = -35.00
[kips]
in tension
Gusset to Girder Interface Forces

Shear force
Vc
 = ( β / r ) Pu
 = -24.17
[kips]
AISC 14th  Eq. 13-2
Axial force
Hc
 = ( ec / r ) Pu
 = -0.51
[kips]
AISC 14th  Eq. 13-3
Moment
Mc
 = Hc ( β - β )
 = 0.00
[kip-ft]
AISC 14th  Eq. 13-19
Gusset to Beam Interface Forces

Shear force
Hb
 = ( α / r ) Pu
 = -24.24
[kips]
AISC 14th  Eq. 13-5
Axial force
Vb
 = ( eb / r ) Pu
 = -0.58
[kips]
AISC 14th  Eq. 13-4
Moment
Mb
 = Vb ( α - α )
 = 0.05
[kip-ft]
AISC 14th  Eq. 13-17
 

Bottom Brace Interface Forces

Refer to AISC 14th  Page 13-4 and Fig. 13-2 for all charts and definitions of variables and symbols shown in calculation below
eb
 = 0.168
[in]
ec
 = 0.148
[in]

α
 = 7.774
[in]
β
 = 6.983
[in]

θ
 = 45.0
[°]

K
 = eb tanθ - ec
 = 0.020
[in]
AISC 14th  Eq. 13-16
D
 = tan2 θ + (
α/β
)2
 = 2.240
AISC 14th  Eq. 13-24
K'
 = α ( tan θ +
α/β
)
 = 16.429
AISC 14th  Eq. 13-23
α
 = [ K' tan θ + K (
α/β
)2 ] / D
 = 7.003
[in]
AISC 14th  Eq. 13-21
β
 = ( K' - K tan θ ) / D
 = 6.983
[in]
AISC 14th  Eq. 13-22
r
 = [ ( eb + β ) 2 + ( ec + α ) 2 ]0.5
 = 10.112
[in]
AISC 14th  Eq. 13-6

Brace axial force
Pu
 = from user input
 = 35.00
[kips]
in compression
Gusset to Girder Interface Forces

Shear force
Vc
 = ( β / r ) Pu
 = 24.17
[kips]
AISC 14th  Eq. 13-2
Axial force
Hc
 = ( ec / r ) Pu
 = 0.51
[kips]
AISC 14th  Eq. 13-3
Moment
Mc
 = Hc ( β - β )
 = 0.00
[kip-ft]
AISC 14th  Eq. 13-19
Gusset to Beam Interface Forces

Shear force
Hb
 = ( α / r ) Pu
 = 24.24
[kips]
AISC 14th  Eq. 13-5
Axial force
Vb
 = ( eb / r ) Pu
 = 0.58
[kips]
AISC 14th  Eq. 13-4
Moment
Mb
 = Vb ( α - α )
 = -0.04
[kip-ft]
AISC 14th  Eq. 13-17
 

Beam to Girder Interface Forces

Beam to Girder Interface Shear Force
Beam end shear reaction
Rb
 = from user input
 = 25.00
[kips]

Top brace gusset-beam axial force
Vb-top
 = 
 = -0.58
[kips]
AISC 14th  Eq. 13-4
Bot brace gusset-beam axial force
Vb-bot
 = 
 = 0.58
[kips]
AISC 14th  Eq. 13-4
Beam to girder shear force
Vb-c
 = Rb + Vb-top - Vb-bot
 = 23.84
[kips]
AISC 14th  Page 13-4
Beam to Girder Interface Axial Force
Top brace gusset-girder axial force
Hc-top
 = 
 = -0.51
[kips]
AISC 14th  Eq. 13-3
Bot brace gusset-girder axial force
Hc-bot
 = 
 = 0.51
[kips]
AISC 14th  Eq. 13-3
Transfer force from adjacent bay
Ab
 = from user input
 = 15.00
[kips]

Beam to girder axial force
Pb-c
 = ( Hc-top + Hc-bot ) x -1 - Ab
 = -15.00
[kips]
AISC 14th  Page 13-4
 

Beam Member Axial Force

This force is not for use in connection calc. It's output here for user input connection forces equilibrium check only.
Pbm - Beam member axial force is different from Pb-c - Beam to girder interface axial force as shown above.

Pbm - Beam member axial force is from structural analysis output and cannot be used directly in beam end to girder connection design as this force is interrupted by brace gusset to beam interface force before beam end reaching the girder. This force is actually not needed from user's input for beam end to girder connection design.

 
Pb-c - Beam to girder interface axial force is calculated from user's input of brace axial forces and trasnfer force using uniform force method. This force is used in the beam end to girder connection design.

 
Pbm - Beam member axial force is not needed for the beam end to girder connection design and is calculated here for verification purpose only. If it matches the structural analysis output, that means equilibrium is reached and user's input of brace axial forces and trasnfer force are correct.

 

Top brace axial force
Pt
 = from user input
 = -35.00
[kips]
in tension
Top brace to ver line angle
θt
 = from user input
 = 45.0
[°]

Top brace gusset-girder axial force
Hct
 = from calc shown above
 = -0.51
[kips]
AISC 14th  Eq. 13-3

Bot brace axial force
Pb
 = from user input
 = 35.00
[kips]
in compression
Bot brace to ver line angle
θb
 = from user input
 = 45.0
[°]

Bot brace gusset-girder axial force
Hcb
 = from calc shown above
 = 0.51
[kips]
AISC 14th  Eq. 13-3

Beam to girder interface axial force
Pb-c
 = from calc shown above
 = -15.00
[kips]
AISC 14th  Page 13-4
 
Beam member axial force
Pbm
 = (Hct - Pt sinθt ) + (Hcb - Pb sinθb )
 = -15.00
[kips]
in tension
+ Pb-c

 

Brace Axial Force Load Case 2

 
Right and left brace force
R Prt
 = 35.00
[kips] (C)
L Plt
 = -35.00
[kips] (T)

Beam end shear & transfer force
Shear Rb
 = 25.00
[kips]
Transfer Ab
 = 15.00
[kips]


 
 

Top Brace Interface Forces

Refer to AISC 14th  Page 13-4 and Fig. 13-2 for all charts and definitions of variables and symbols shown in calculation below
eb
 = 0.168
[in]
ec
 = 0.148
[in]

α
 = 7.951
[in]
β
 = 6.983
[in]

θ
 = 45.0
[°]

K
 = eb tanθ - ec
 = 0.020
[in]
AISC 14th  Eq. 13-16
D
 = tan2 θ + (
α/β
)2
 = 2.297
AISC 14th  Eq. 13-24
K'
 = α ( tan θ +
α/β
)
 = 17.005
AISC 14th  Eq. 13-23
α
 = [ K' tan θ + K (
α/β
)2 ] / D
 = 7.003
[in]
AISC 14th  Eq. 13-21
β
 = ( K' - K tan θ ) / D
 = 6.983
[in]
AISC 14th  Eq. 13-22
r
 = [ ( eb + β ) 2 + ( ec + α ) 2 ]0.5
 = 10.112
[in]
AISC 14th  Eq. 13-6

Brace axial force
Pu
 = from user input
 = 35.00
[kips]
in compression
Gusset to Girder Interface Forces

Shear force
Vc
 = ( β / r ) Pu
 = 24.17
[kips]
AISC 14th  Eq. 13-2
Axial force
Hc
 = ( ec / r ) Pu
 = 0.51
[kips]
AISC 14th  Eq. 13-3
Moment
Mc
 = Hc ( β - β )
 = 0.00
[kip-ft]
AISC 14th  Eq. 13-19
Gusset to Beam Interface Forces

Shear force
Hb
 = ( α / r ) Pu
 = 24.24
[kips]
AISC 14th  Eq. 13-5
Axial force
Vb
 = ( eb / r ) Pu
 = 0.58
[kips]
AISC 14th  Eq. 13-4
Moment
Mb
 = Vb ( α - α )
 = -0.05
[kip-ft]
AISC 14th  Eq. 13-17
 

Bottom Brace Interface Forces

Refer to AISC 14th  Page 13-4 and Fig. 13-2 for all charts and definitions of variables and symbols shown in calculation below
eb
 = 0.168
[in]
ec
 = 0.148
[in]

α
 = 7.774
[in]
β
 = 6.983
[in]

θ
 = 45.0
[°]

K
 = eb tanθ - ec
 = 0.020
[in]
AISC 14th  Eq. 13-16
D
 = tan2 θ + (
α/β
)2
 = 2.240
AISC 14th  Eq. 13-24
K'
 = α ( tan θ +
α/β
)
 = 16.429
AISC 14th  Eq. 13-23
α
 = [ K' tan θ + K (
α/β
)2 ] / D
 = 7.003
[in]
AISC 14th  Eq. 13-21
β
 = ( K' - K tan θ ) / D
 = 6.983
[in]
AISC 14th  Eq. 13-22
r
 = [ ( eb + β ) 2 + ( ec + α ) 2 ]0.5
 = 10.112
[in]
AISC 14th  Eq. 13-6

Brace axial force
Pu
 = from user input
 = -35.00
[kips]
in tension
Gusset to Girder Interface Forces

Shear force
Vc
 = ( β / r ) Pu
 = -24.17
[kips]
AISC 14th  Eq. 13-2
Axial force
Hc
 = ( ec / r ) Pu
 = -0.51
[kips]
AISC 14th  Eq. 13-3
Moment
Mc
 = Hc ( β - β )
 = 0.00
[kip-ft]
AISC 14th  Eq. 13-19
Gusset to Beam Interface Forces

Shear force
Hb
 = ( α / r ) Pu
 = -24.24
[kips]
AISC 14th  Eq. 13-5
Axial force
Vb
 = ( eb / r ) Pu
 = -0.58
[kips]
AISC 14th  Eq. 13-4
Moment
Mb
 = Vb ( α - α )
 = 0.04
[kip-ft]
AISC 14th  Eq. 13-17
 

Beam to Girder Interface Forces

Beam to Girder Interface Shear Force
Beam end shear reaction
Rb
 = from user input
 = 25.00
[kips]

Top brace gusset-beam axial force
Vb-top
 = 
 = 0.58
[kips]
AISC 14th  Eq. 13-4
Bot brace gusset-beam axial force
Vb-bot
 = 
 = -0.58
[kips]
AISC 14th  Eq. 13-4
Beam to girder shear force
Vb-c
 = Rb + Vb-top - Vb-bot
 = 26.16
[kips]
AISC 14th  Page 13-4
Beam to Girder Interface Axial Force
Top brace gusset-girder axial force
Hc-top
 = 
 = 0.51
[kips]
AISC 14th  Eq. 13-3
Bot brace gusset-girder axial force
Hc-bot
 = 
 = -0.51
[kips]
AISC 14th  Eq. 13-3
Transfer force from adjacent bay
Ab
 = from user input
 = 15.00
[kips]

Beam to girder axial force
Pb-c
 = ( Hc-top + Hc-bot ) x -1 - Ab
 = -15.00
[kips]
AISC 14th  Page 13-4
 

Beam Member Axial Force

This force is not for use in connection calc. It's output here for user input connection forces equilibrium check only.
Pbm - Beam member axial force is different from Pb-c - Beam to girder interface axial force as shown above.

Pbm - Beam member axial force is from structural analysis output and cannot be used directly in beam end to girder connection design as this force is interrupted by brace gusset to beam interface force before beam end reaching the girder. This force is actually not needed from user's input for beam end to girder connection design.

 
Pb-c - Beam to girder interface axial force is calculated from user's input of brace axial forces and trasnfer force using uniform force method. This force is used in the beam end to girder connection design.

 
Pbm - Beam member axial force is not needed for the beam end to girder connection design and is calculated here for verification purpose only. If it matches the structural analysis output, that means equilibrium is reached and user's input of brace axial forces and trasnfer force are correct.

 

Top brace axial force
Pt
 = from user input
 = 35.00
[kips]
in compression
Top brace to ver line angle
θt
 = from user input
 = 45.0
[°]

Top brace gusset-girder axial force
Hct
 = from calc shown above
 = 0.51
[kips]
AISC 14th  Eq. 13-3

Bot brace axial force
Pb
 = from user input
 = -35.00
[kips]
in tension
Bot brace to ver line angle
θb
 = from user input
 = 45.0
[°]

Bot brace gusset-girder axial force
Hcb
 = from calc shown above
 = -0.51
[kips]
AISC 14th  Eq. 13-3

Beam to girder interface axial force
Pb-c
 = from calc shown above
 = -15.00
[kips]
AISC 14th  Page 13-4
 
Beam member axial force
Pbm
 = (Hct - Pt sinθt ) + (Hcb - Pb sinθb )
 = -15.00
[kips]
in tension
+ Pb-c

 
 
Right Brace - Brace to Gusset
Sect=2L31⁄2 x 31⁄2 x 1⁄2
PLC1 =-35.00 kips (T)
PLC2 =35.00 kips (C)
Code=AISC 360-10 LRFD
 
Result Summary
geometries & weld limitations = PASS
limit states max ratio 
= 0.92
PASS
 
 
Geometry Restriction Checks - Double Angle to Gusset
PASS
Min Bolt Edge Distance - Double Angle to Gusset

Bolt diameter
db
 = 
 = 0.750
[in]

Min edge distance allowed
Le-min
 = 
 = 1.000
[in]
AISC 14th  Table J3.4
Min edge distance in Double Angle to Gusset
Le
 = 
 = 1.375
[in]

 > Le-min
OK
Min Bolt Spacing - Double Angle to Gusset

Bolt diameter
db
 = 
 = 0.750
[in]

Min bolt spacing allowed
Ls-min
 = 2.667 db
 = 2.000
[in]
AISC 14th  J3.3
Min Bolt spacing in Double Angle to Gusset
Ls
 = 
 = 3.000
[in]

 > Ls-min
OK
 
 
 
 
Brace Force Load Case 1
Sect=2L31⁄2 x 31⁄2 x 1⁄2
P =-35.00 kips (T)
ratio = 0.92
PASS
Double Angle Brace - Tensile Yield
ratio = 35.00 / 292.50
= 0.12
PASS
Gross area subject to tension
Ag
 = 
 = 6.500
[in2]

Steel yield strength
Fy
 = 
 = 50.0
[ksi]

Tensile force required
Pu
 = 
 = 35.00
[kips]

Tensile yielding strength
Rn
 = Fy Ag
 = 325.00
[kips]
AISC 14th  Eq D2-1
Resistance factor-LRFD
φ
 = 0.90
AISC 14th  D2 (a)
φ Rn
 = 
 = 292.50
[kips]
AISC 14th  Eq D2-1
ratio
 = 0.12
 > Pu
OK
 
Double Angle Brace - Tensile Rupture
ratio = 35.00 / 178.24
= 0.20
PASS
Section gross area
Ag
 = 2L31⁄2 x 31⁄2 x 1⁄2
 = 6.500
[in2]

Bolt hole diameter
bolt dia db
 = 3⁄4
[in]
bolt hole dia dh
 = 7⁄8
[in]
AISC 14th  B4.3b
Number of bolt row
nv
 = 1
angle leg t
 = 0.500
[in]

Tensile net area
An
 = Ag - nv dh t x 2
 = 5.625
[in2]


No of bolt column
nh
 = 2
bolt space sh
 = 3.000
[in]

Length of connection
L
 = ( nh -1 ) sh
 = 3.000
[in]

Eccentricity of connection
x
 = from sect L31⁄2 x 31⁄2 x 1⁄2
 = 1.050
[in]

Shear lag factor
U
 = 1 - x / L
 = 0.650
AISC 14th  Table D3.1

Tensile force required
Pu
 = 
 = 35.00
[kips]

Tensile effective net area
Ae
 = An U
 = 3.656
[in2]

Plate tensile strength
Fu
 = 
 = 65.0
[ksi]

Tensile rupture strength
Rn
 = Fu Ae
 = 237.66
[kips]
AISC 14th  Eq D2-2
Resistance factor-LRFD
φ
 = 0.75
AISC 14th  D2 (b)
φ Rn
 = 
 = 178.24
[kips]
AISC 14th  Eq D2-2
ratio
 = 0.20
 > Pu
OK
 
 
Double Angle Brace - Bolt Shear
ratio = 17.50 / 35.78
= 0.49
PASS
Bolt shear stress
bolt grade
 = A325-N
Fnv
 = 54.0
[ksi]
AISC 14th  Table J3.2
bolt dia db
 = 0.750
[in]
bolt area Ab
 = 0.442
[in2]

Number of bolt carried shear
ns
 = 2.0
shear plane m
 = 1

Bolt group eccentricity coefficient
Cec
 = 
 = 1.000

Required shear strength
Vu
 = 
 = 17.50
[kips]

Bolt shear strength
Rn
 = Fnv Ab ns m Cec
 = 47.71
[kips]
AISC 14th  Eq J3-1
Bolt resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq J3-1
φ Rn
 = 
 = 35.78
[kips]

ratio
 = 0.49
 > Vu
OK
 
Double Angle Brace - Slip Critical - Angle/Gusset Plate
ratio = 17.50 / 18.98
= 0.92
PASS
Bolt dia & bolt pretension
dia db
 = 3⁄4
[in]
Pretension Tb
 = 28.00
[kips]
AISC 14th  Table J3.1
Surface class
 = Class A
Slip coeff. μ
 = 0.30
AISC 14th  J3.8
Min. bolt pretension
Du
 = 1.13
Filler factor hf
 = 1.00
AISC 14th  J3.8
No of bolt row & column
nr
 = 1
nc
 = 2

No of slip plane
ns
 = 1

Bolt group eccentricity coefficient
Cec
 = 
 = 1.000

Required shear strength
Vu
 = 
 = 17.50
[kips]

Slip resistance
Rn
 = μ Du hf Tb ns nr nc Cec
 = 18.98
[kips]
AISC 14th  Eq J3-4
Resistance factor-LRFD
φ
 = 1.00
for standard size or SSLT hole
AISC 14th  J3.8
φ Rn
 = 
 = 18.98
[kips]

ratio
 = 0.92
 > Vu
OK
 
Double Angle Brace - Bolt Bearing on Angle
ratio = 17.50 / 35.78
= 0.49
PASS
Single Bolt Shear Strength

Bolt shear stress
bolt grade
 = A325-N
Fnv
 = 54.0
[ksi]
AISC 14th  Table J3.2
bolt dia db
 = 0.750
[in]
bolt area Ab
 = 0.442
[in2]

Single bolt shear strength
Rn-bolt
 = Fnv Ab
 = 23.86
[kips]
AISC 14th  Eq J3-1
Bolt Bearing/TearOut Strength on Plate


Bolt hole diameter
bolt dia db
 = 3⁄4
[in]
bolt hole dia dh
 = 13⁄16
[in]
AISC 14th  Table J3.3
Bolt spacing & edge distance
spacing Ls
 = 3.000
[in]
edge distance Le
 = 1.375
[in]

Plate tensile strength
Fu
 = 65.0
[ksi]

Plate thickness
t
 = 0.500
[in]

Interior Bolt


Bolt hole edge clear distance
Lc
 = Ls - dh
 = 2.188
[in]

Bolt tear out/bearing strength
Rn-t&b-in
 = 1.5 Lc t Fu ≤ 3.0 db t Fu
AISC 14th  Eq J3-6b
 = 106.64 ≤ 73.13
 = 73.13
[kips]

Bolt strength at interior
Rn-in
 = min ( Rn-t&b-in , Rn-bolt )
 = 23.86
[kips]

Edge Bolt


Bolt hole edge clear distance
Lc
 = Le - dh / 2
 = 0.969
[in]

Bolt tear out/bearing strength
Rn-t&b-ed
 = 1.5 Lc t Fu ≤ 3.0 db t Fu
AISC 14th  Eq J3-6b
 = 47.23 ≤ 73.13
 = 47.23
[kips]

Bolt strength at edge
Rn-ed
 = min ( Rn-t&b-ed , Rn-bolt )
 = 23.86
[kips]


Number of bolt
interior nin
 = 1
edge ned
 = 1

Bolt bearing strength for all bolts
Rn
 = nin Rn-in + ned Rn-ed
 = 47.71
[kips]

Required shear strength
Vu
 = 
 = 17.50
[kips]

Bolt resistance factor-LRFD
φ
 = 0.75
AISC 14th  J3-10
φ Rn
 = 
 = 35.78
[kips]

ratio
 = 0.49
 > Vu
OK
 
Double Angle Brace - Bolt Bearing on Gusset Plate
ratio = 17.50 / 35.78
= 0.49
PASS
Single Bolt Shear Strength

Bolt shear stress
bolt grade
 = A325-N
Fnv
 = 54.0
[ksi]
AISC 14th  Table J3.2
bolt dia db
 = 0.750
[in]
bolt area Ab
 = 0.442
[in2]

Single bolt shear strength
Rn-bolt
 = Fnv Ab
 = 23.86
[kips]
AISC 14th  Eq J3-1
Bolt Bearing/TearOut Strength on Plate


Bolt hole diameter
bolt dia db
 = 3⁄4
[in]
bolt hole dia dh
 = 13⁄16
[in]
AISC 14th  Table J3.3
Bolt spacing & edge distance
spacing Ls
 = 3.000
[in]
edge distance Le
 = 1.625
[in]

Plate tensile strength
Fu
 = 65.0
[ksi]

Plate thickness
t
 = 0.375
[in]

Interior Bolt


Bolt hole edge clear distance
Lc
 = Ls - dh
 = 2.188
[in]

Bolt tear out/bearing strength
Rn-t&b-in
 = 1.5 Lc t Fu ≤ 3.0 db t Fu
AISC 14th  Eq J3-6b
 = 79.98 ≤ 54.84
 = 54.84
[kips]

Bolt strength at interior
Rn-in
 = min ( Rn-t&b-in , Rn-bolt )
 = 23.86
[kips]

Edge Bolt


Bolt hole edge clear distance
Lc
 = Le - dh / 2
 = 1.219
[in]

Bolt tear out/bearing strength
Rn-t&b-ed
 = 1.5 Lc t Fu ≤ 3.0 db t Fu
AISC 14th  Eq J3-6b
 = 44.56 ≤ 54.84
 = 44.56
[kips]

Bolt strength at edge
Rn-ed
 = min ( Rn-t&b-ed , Rn-bolt )
 = 23.86
[kips]


Number of bolt
interior nin
 = 1
edge ned
 = 1

Bolt bearing strength for all bolts
Rn
 = nin Rn-in + ned Rn-ed
 = 47.71
[kips]

Required shear strength
Vu
 = 
 = 17.50
[kips]

Bolt resistance factor-LRFD
φ
 = 0.75
AISC 14th  J3-10
φ Rn
 = 
 = 35.78
[kips]

ratio
 = 0.49
 > Vu
OK
 
Double Angle Brace - Block Shear - 1-Side Strip
ratio = 17.50 / 70.69
= 0.25
PASS
Plate Block Shear - Side Strip


Bolt hole diameter
bolt dia db
 = 3⁄4
[in]
bolt hole dia dh
 = 7⁄8
[in]
AISC 14th  B4.3b
Plate thickness
tp
 = 0.500
[in]

Plate strength
Fy
 = 50.0
[ksi]
Fu
 = 65.0
[ksi]

Bolt no in ver & hor dir
nv
 = 1
nh
 = 2

Bolt spacing in hor dir
sh
 = 3.000
[in]

Bolt edge dist in ver & hor dir
ev
 = 1.500
[in]
eh
 = 1.375
[in]


Gross area subject to shear
Agv
 = [ (nh - 1) sh + eh ] tp
 = 2.188
[in2]

Net area subject to shear
Anv
 = Agv - [ (nh - 1) + 0.5 ] dh tp
 = 1.531
[in2]

Net area subject to tension
Ant
 = ( ev - 0.5 dh ) tp
 = 0.531
[in2]


Block shear strength required
Vu
 = 
 = 17.50
[kips]

Uniform tension stress factor
Ubs
 = 1.00
AISC 14th  Fig C-J4.2
Bolt shear resistance provided
Rn
 = min (0.6Fu Anv , 0.6Fy Agv ) +
 = 94.25
[kips]
AISC 14th  Eq J4-5
Ubs Fu Ant

Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq J4-5
φ Rn
 = 
 = 70.69
[kips]

ratio
 = 0.25
 > Vu
OK
 
 
Gusset Plate - Tensile Yield (Whitmore)
ratio = 35.00 / 125.96
= 0.28
PASS
Plate Tensile Yielding Check


Plate size
width bp
 = 7.464
[in]
thickness tp
 = 0.375
[in]

Plate yield strength
Fy
 = 50.0
[ksi]

Plate gross area in shear
Ag
 = bp tp
 = 2.799
[in2]

Tensile force required
Pu
 = 
 = 35.00
[kips]

Plate tensile yielding strength
Rn
 = Fy Ag
 = 139.95
[kips]
AISC 14th  Eq J4-1
Resistance factor-LRFD
φ
 = 0.90
AISC 14th  Eq J4-1
φ Rn
 = 
 = 125.96
[kips]

ratio
 = 0.28
 > Pu
OK
 
Gusset Plate - Tensile Rupture (Whitmore)
ratio = 35.00 / 104.46
= 0.34
PASS
Plate Tensile Rupture Check


Bolt hole diameter
bolt dia db
 = 3⁄4
[in]
bolt hole dia dh
 = 7⁄8
[in]
AISC 14th  B4.3b
Number of bolt
n
 = 2

Plate size
width bp
 = 7.464
[in]
thickness tp
 = 0.375
[in]

Plate tensile strength
Fu
 = 65.0
[ksi]

Plate net area in tension
Ant
 = ( bp - n dh ) tp
 = 2.143
[in2]

Tensile force required
Pu
 = 
 = 35.00
[kips]

Plate tensile rupture strength
Rn
 = Fu Ant
 = 139.28
[kips]
AISC 14th  Eq J4-2
Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq J4-2
φ Rn
 = 
 = 104.46
[kips]
AISC 14th  Eq J4-2
ratio
 = 0.34
 > Pu
OK
 
Gusset Plate - Block Shear - Center Strip
ratio = 35.00 / 129.80
= 0.27
PASS
Plate Block Shear - Center Strip


Bolt hole diameter
bolt dia db
 = 3⁄4
[in]
bolt hole dia dh
 = 7⁄8
[in]
AISC 14th  B4.3b
Plate thickness
tp
 = 0.375
[in]

Plate strength
Fy
 = 50.0
[ksi]
Fu
 = 65.0
[ksi]

Bolt no in ver & hor dir
nv
 = 2.0
nh
 = 2

Bolt spacing in hor dir
sh
 = 3.000
[in]
edge dist eh
 = 1.625
[in]

Width of block shear strip
Wbs
 = 4.000
[in]


Gross area subject to shear
Agv
 = [ (nh - 1) sh + eh ] tp x 2
 = 3.469
[in2]

Net area subject to shear
Anv
 = Agv - [(nh - 1)+ 0.5] dh tp x2
 = 2.484
[in2]

Net area subject to tension
when sheared out by center strip
Ant
 = [ Wbs - (nv - 1) dh ] tp
 = 1.172
[in2]


Block shear strength required
Vu
 = 
 = 35.00
[kips]

Uniform tension stress factor
Ubs
 = 1.00
AISC 14th  Fig C-J4.2
Bolt shear resistance provided
Rn
 = min (0.6Fu Anv , 0.6Fy Agv ) +
 = 173.06
[kips]
AISC 14th  Eq J4-5
Ubs Fu Ant

Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq J4-5
φ Rn
 = 
 = 129.80
[kips]

ratio
 = 0.27
 > Vu
OK
 
 
 
Brace Force Load Case 2
Sect=2L31⁄2 x 31⁄2 x 1⁄2
P =35.00 kips (C)
ratio = 0.92
PASS
Double Angle Brace - Bolt Shear
ratio = 17.50 / 35.78
= 0.49
PASS
Bolt shear stress
bolt grade
 = A325-N
Fnv
 = 54.0
[ksi]
AISC 14th  Table J3.2
bolt dia db
 = 0.750
[in]
bolt area Ab
 = 0.442
[in2]

Number of bolt carried shear
ns
 = 2.0
shear plane m
 = 1

Bolt group eccentricity coefficient
Cec
 = 
 = 1.000

Required shear strength
Vu
 = 
 = 17.50
[kips]

Bolt shear strength
Rn
 = Fnv Ab ns m Cec
 = 47.71
[kips]
AISC 14th  Eq J3-1
Bolt resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq J3-1
φ Rn
 = 
 = 35.78
[kips]

ratio
 = 0.49
 > Vu
OK
 
Double Angle Brace - Slip Critical - Angle/Gusset Plate
ratio = 17.50 / 18.98
= 0.92
PASS
Bolt dia & bolt pretension
dia db
 = 3⁄4
[in]
Pretension Tb
 = 28.00
[kips]
AISC 14th  Table J3.1
Surface class
 = Class A
Slip coeff. μ
 = 0.30
AISC 14th  J3.8
Min. bolt pretension
Du
 = 1.13
Filler factor hf
 = 1.00
AISC 14th  J3.8
No of bolt row & column
nr
 = 1
nc
 = 2

No of slip plane
ns
 = 1

Bolt group eccentricity coefficient
Cec
 = 
 = 1.000

Required shear strength
Vu
 = 
 = 17.50
[kips]

Slip resistance
Rn
 = μ Du hf Tb ns nr nc Cec
 = 18.98
[kips]
AISC 14th  Eq J3-4
Resistance factor-LRFD
φ
 = 1.00
for standard size or SSLT hole
AISC 14th  J3.8
φ Rn
 = 
 = 18.98
[kips]

ratio
 = 0.92
 > Vu
OK
 
Double Angle Brace - Bolt Bearing on Angle
ratio = 17.50 / 35.78
= 0.49
PASS
Single Bolt Shear Strength

Bolt shear stress
bolt grade
 = A325-N
Fnv
 = 54.0
[ksi]
AISC 14th  Table J3.2
bolt dia db
 = 0.750
[in]
bolt area Ab
 = 0.442
[in2]

Single bolt shear strength
Rn-bolt
 = Fnv Ab
 = 23.86
[kips]
AISC 14th  Eq J3-1
Bolt Bearing/TearOut Strength on Plate


Bolt hole diameter
bolt dia db
 = 3⁄4
[in]
bolt hole dia dh
 = 13⁄16
[in]
AISC 14th  Table J3.3
Bolt spacing
spacing Ls
 = 3.000
[in]

Plate tensile strength
Fu
 = 65.0
[ksi]

Plate thickness
t
 = 0.500
[in]

Interior Bolt


Bolt hole edge clear distance
Lc
 = Ls - dh
 = 2.188
[in]

Bolt tear out/bearing strength
Rn-t&b-in
 = 1.5 Lc t Fu ≤ 3.0 db t m Fu
AISC 14th  Eq J3-6b
 = 106.64 ≤ 73.13
 = 73.13
[kips]

Bolt strength at interior
Rn-in
 = min ( Rn-t&b-in , Rn-bolt )
 = 23.86
[kips]


Number of bolt
interior nin
 = 2

Bolt bearing strength for all bolts
Rn
 = nin Rn-in
 = 47.71
[kips]

Required shear strength
Vu
 = 
 = 17.50
[kips]

Bolt resistance factor-LRFD
φ
 = 0.75
AISC 14th  J3-10
φ Rn
 = 
 = 35.78
[kips]

ratio
 = 0.49
 > Vu
OK
 
Double Angle Brace - Bolt Bearing on Gusset Plate
ratio = 17.50 / 35.78
= 0.49
PASS
Single Bolt Shear Strength

Bolt shear stress
bolt grade
 = A325-N
Fnv
 = 54.0
[ksi]
AISC 14th  Table J3.2
bolt dia db
 = 0.750
[in]
bolt area Ab
 = 0.442
[in2]

Single bolt shear strength
Rn-bolt
 = Fnv Ab
 = 23.86
[kips]
AISC 14th  Eq J3-1
Bolt Bearing/TearOut Strength on Plate


Bolt hole diameter
bolt dia db
 = 3⁄4
[in]
bolt hole dia dh
 = 13⁄16
[in]
AISC 14th  Table J3.3
Bolt spacing
spacing Ls
 = 3.000
[in]

Plate tensile strength
Fu
 = 65.0
[ksi]

Plate thickness
t
 = 0.375
[in]

Interior Bolt


Bolt hole edge clear distance
Lc
 = Ls - dh
 = 2.188
[in]

Bolt tear out/bearing strength
Rn-t&b-in
 = 1.5 Lc t Fu ≤ 3.0 db t m Fu
AISC 14th  Eq J3-6b
 = 79.98 ≤ 54.84
 = 54.84
[kips]

Bolt strength at interior
Rn-in
 = min ( Rn-t&b-in , Rn-bolt )
 = 23.86
[kips]


Number of bolt
interior nin
 = 2

Bolt bearing strength for all bolts
Rn
 = nin Rn-in
 = 47.71
[kips]

Required shear strength
Vu
 = 
 = 17.50
[kips]

Bolt resistance factor-LRFD
φ
 = 0.75
AISC 14th  J3-10
φ Rn
 = 
 = 35.78
[kips]

ratio
 = 0.49
 > Vu
OK
 
 
Gusset Plate - Compression (Whitmore)
ratio = 35.00 / 103.42
= 0.34
PASS
Plate Compression Check


Plate size
width bp
 = 7.464
[in]
thickness tp
 = 0.375
[in]

Fy
 = 50.0
[ksi]
E
 = 29000
[ksi]

Plate gross area in compression
Ag
 = bp tp
 = 2.799
[in2]


Plate radius of gyration
r
 = tp / √12
 = 0.108
[in]

Plate effective length factor
K
 = 
 = 0.50
Plate unbraced length
Lu
 = 
 = 11.242
[in]

Plate slenderness
KL/r
 = 0.50 x Lu  / r
 = 51.92


when  
KL/r
  >  25 , use Chapter E
AISC 14th  J4.4 (b)
Elastic buckling stress
Fe
 = 
π2 E/( KL/r )2
 = 106.16
[ksi]
AISC 14th  Eq E3-4
when  
KL/r
  ≤ 4.71 (
E/Fy
) 0.5 = 113.43
AISC 14th  E3 (a)
Critical stress
Fcr
 = 0.658 ( Fy / Fe )   Fy
 = 41.05
[ksi]
AISC 14th  Eq E3-2

Plate compression required
Pu
 = 
 = 35.00
[kips]

Plate compression provided
Rn
 = Fcr x Ag
 = 114.91
[kips]
AISC 14th  Eq E3-1
Bolt resistance factor-LRFD
φ
 = 0.90
AISC 14th  E1
φ Rn
 = 
 = 103.42
[kips]

ratio
 = 0.34
 > Pu
OK
 
 
Right Brace - Gusset to Girder
End Plate Connection
Code=AISC 360-10 LRFD
 
Result Summary
geometries & weld limitations = PASS
limit states max ratio 
= 0.64
PASS
 
 
Geometry Restriction Checks - End Plate to Column Web
PASS
Min Bolt Edge Distance - End Plate to Column Web

Bolt diameter
db
 = 
 = 0.750
[in]

Min edge distance allowed
Le-min
 = 
 = 1.000
[in]
AISC 14th  Table J3.4
Min edge distance in End Plate to Column Web
Le
 = 
 = 1.375
[in]

 > Le-min
OK
Min Bolt Spacing - End Plate to Column Web

Bolt diameter
db
 = 
 = 0.750
[in]

Min bolt spacing allowed
Ls-min
 = 2.667 db
 = 2.000
[in]
AISC 14th  J3.3
Min Bolt spacing in End Plate to Column Web
Ls
 = 
 = 3.000
[in]

 > Ls-min
OK
 
Weld Limitation Checks - Gusset Plate to End Plate
PASS
Min Fillet Weld Size

Thinner part joined thickness
t
 = 
 = 0.375
[in]

Min fillet weld size allowed
wmin
 = 
 = 0.188
[in]
AISC 14th  Table J2.4
Fillet weld size provided
w
 = 
 = 0.313
[in]

 > wmin
OK
Min Fillet Weld Length

Fillet weld size provided
w
 = 
 = 0.313
[in]

Min fillet weld length allowed
Lmin
 = 4 x w
 = 1.250
[in]
AISC 14th  J2.2b
Min fillet weld length
L
 = 
 = 9.108
[in]

 > Lmin
OK
 
 
 
 
Brace Force Load Case 1
Gusset plate t=0.375
P =-35.00 kips (T)
ratio = 0.64
PASS
Gusset Plate - Shear Yielding
ratio = 24.17 / 102.47
= 0.24
PASS
Plate Shear Yielding Check


Plate size
width bp
 = 9.108
[in]
thickness tp
 = 0.375
[in]

Plate yield strength
Fy
 = 50.0
[ksi]

Plate gross area in shear
Agv
 = bp tp
 = 3.416
[in2]

Shear force required
Vu
 = 
 = 24.17
[kips]

Plate shear yielding strength
Rn
 = 0.6 Fy Agv
 = 102.47
[kips]
AISC 14th  Eq J4-3
Resistance factor-LRFD
φ
 = 1.00
AISC 14th  Eq J4-3
φ Rn
 = 
 = 102.47
[kips]

ratio
 = 0.24
 > Vu
OK
 
Gusset Plate - Shear Rupture
ratio = 24.17 / 99.90
= 0.24
PASS
Plate Shear Rupture Check


Plate size
width bp
 = 9.108
[in]
thickness tp
 = 0.375
[in]

Plate tensile strength
Fu
 = 65.0
[ksi]

Plate net area in shear
Anv
 = bp tp
 = 3.416
[in2]

Shear force in demand
Vu
 = 
 = 24.17
[kips]

Plate shear rupture strength
Rn
 = 0.6 Fu Anv
 = 133.20
[kips]
AISC 14th  Eq J4-4
Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq J4-4
φ Rn
 = 
 = 99.90
[kips]

ratio
 = 0.24
 > Vu
OK
 
 
End Plate - Shear Yield
ratio = 12.09 / 64.69
= 0.19
PASS
Plate Shear Yielding Check


Plate size
width bp
 = 5.750
[in]
thickness tp
 = 0.375
[in]

Plate yield strength
Fy
 = 50.0
[ksi]

Plate gross area in shear
Agv
 = bp tp
 = 2.156
[in2]

Shear force required
Vu
 = 
 = 12.09
[kips]

Plate shear yielding strength
Rn
 = 0.6 Fy Agv
 = 64.69
[kips]
AISC 14th  Eq J4-3
Resistance factor-LRFD
φ
 = 1.00
AISC 14th  Eq J4-3
φ Rn
 = 
 = 64.69
[kips]

ratio
 = 0.19
 > Vu
OK
 
End Plate - Shear Rupture
ratio = 12.09 / 43.88
= 0.28
PASS
Plate Shear Rupture Check


Bolt hole diameter
bolt dia db
 = 3⁄4
[in]
bolt hole dia dh
 = 7⁄8
[in]
AISC 14th  B4.3b
Number of bolt
n
 = 2

Plate size
width bp
 = 5.750
[in]
thickness tp
 = 0.375
[in]

Plate tensile strength
Fu
 = 65.0
[ksi]

Plate net area in shear
Anv
 = ( bp - n dh ) tp
 = 1.500
[in2]

Shear force required
Vu
 = 
 = 12.09
[kips]

Plate shear rupture strength
Rn
 = 0.6 Fu Anv
 = 58.50
[kips]
AISC 14th  Eq J4-4
Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq J4-4
φ Rn
 = 
 = 43.88
[kips]

ratio
 = 0.28
 > Vu
OK
 
End Plate - Block Shear - Center Strip
ratio = 24.17 / 124.31
= 0.19
PASS
Plate Block Shear - Center Strip


Bolt hole diameter
bolt dia db
 = 3⁄4
[in]
bolt hole dia dh
 = 7⁄8
[in]
AISC 14th  B4.3b
Plate thickness
tp
 = 0.375
[in]

Plate strength
Fy
 = 50.0
[ksi]
Fu
 = 65.0
[ksi]

Bolt no in ver & hor dir
nv
 = 2
nh
 = 2

Bolt spacing in ver & hor dir
sv
 = 4.000
[in]
sh
 = 3.000
[in]

Bolt edge dist in ver & hor dir
ev
 = 1.375
[in]
eh
 = 1.375
[in]


Gross area subject to shear
Agv
 = [ (nh - 1) sh + eh ] tp x 2
 = 3.281
[in2]

Net area subject to shear
Anv
 = Agv - [(nh - 1)+ 0.5] dh tp x2
 = 2.297
[in2]

Net area subject to tension
when sheared out by center strip
Ant
 = ( nv - 1) ( sv - dh ) tp
 = 1.172
[in2]


Block shear strength required
Vu
 = 
 = 24.17
[kips]

Uniform tension stress factor
Ubs
 = 1.00
AISC 14th  Fig C-J4.2
Bolt shear resistance provided
Rn
 = min (0.6Fu Anv , 0.6Fy Agv ) +
 = 165.75
[kips]
AISC 14th  Eq J4-5
Ubs Fu Ant

Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq J4-5
φ Rn
 = 
 = 124.31
[kips]

ratio
 = 0.19
 > Vu
OK
 
End Plate - Block Shear - 2-Side Strip
ratio = 24.17 / 101.46
= 0.24
PASS
Plate Block Shear - 2 Side Strips


Bolt hole diameter
bolt dia db
 = 3⁄4
[in]
bolt hole dia dh
 = 7⁄8
[in]
AISC 14th  B4.3b
Plate thickness
tp
 = 0.375
[in]

Plate strength
Fy
 = 50.0
[ksi]
Fu
 = 65.0
[ksi]

Bolt no in ver & hor dir
nv
 = 2
nh
 = 2

Bolt spacing in ver & hor dir
sv
 = 4.000
[in]
sh
 = 3.000
[in]

Bolt edge dist in ver & hor dir
ev
 = 1.375
[in]
eh
 = 1.375
[in]


Gross area subject to shear
Agv
 = [ (nh - 1) sh + eh ] tp x 2
 = 3.281
[in2]

Net area subject to shear
Anv
 = Agv - [(nh - 1)+ 0.5] dh tp x2
 = 2.297
[in2]

Net area subject to tension
when sheared out by 2 side strips
Ant
 = ( ev - 0.5 dh ) tp x 2
 = 0.703
[in2]


Block shear strength required
Vu
 = 
 = 24.17
[kips]

Uniform tension stress factor
Ubs
 = 1.00
AISC 14th  Fig C-J4.2
Bolt shear resistance provided
Rn
 = min (0.6Fu Anv , 0.6Fy Agv ) +
 = 135.28
[kips]
AISC 14th  Eq J4-5
Ubs Fu Ant

Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq J4-5
φ Rn
 = 
 = 101.46
[kips]

ratio
 = 0.24
 > Vu
OK
 
End Plate - Bolt Bearing on End Plate
ratio = 24.17 / 71.57
= 0.34
PASS
Single Bolt Shear Strength

Bolt shear stress
bolt grade
 = A325-N
Fnv
 = 54.0
[ksi]
AISC 14th  Table J3.2
bolt dia db
 = 0.750
[in]
bolt area Ab
 = 0.442
[in2]

Single bolt shear strength
Rn-bolt
 = Fnv Ab
 = 23.86
[kips]
AISC 14th  Eq J3-1
Bolt Bearing/TearOut Strength on Plate


Bolt hole diameter
bolt dia db
 = 3⁄4
[in]
bolt hole dia dh
 = 13⁄16
[in]
AISC 14th  Table J3.3
Bolt spacing & edge distance
spacing Ls
 = 3.000
[in]
edge distance Le
 = 1.375
[in]

Plate tensile strength
Fu
 = 65.0
[ksi]

Plate thickness
t
 = 0.375
[in]

Interior Bolt


Bolt hole edge clear distance
Lc
 = Ls - dh
 = 2.188
[in]

Bolt tear out/bearing strength
Rn-t&b-in
 = 1.5 Lc t Fu ≤ 3.0 db t Fu
AISC 14th  Eq J3-6b
 = 79.98 ≤ 54.84
 = 54.84
[kips]

Bolt strength at interior
Rn-in
 = min ( Rn-t&b-in , Rn-bolt )
 = 23.86
[kips]

Edge Bolt


Bolt hole edge clear distance
Lc
 = Le - dh / 2
 = 0.969
[in]

Bolt tear out/bearing strength
Rn-t&b-ed
 = 1.5 Lc t Fu ≤ 3.0 db t Fu
AISC 14th  Eq J3-6b
 = 35.42 ≤ 54.84
 = 35.42
[kips]

Bolt strength at edge
Rn-ed
 = min ( Rn-t&b-ed , Rn-bolt )
 = 23.86
[kips]


Number of bolt
interior nin
 = 2
edge ned
 = 2

Bolt bearing strength for all bolts
Rn
 = nin Rn-in + ned Rn-ed
 = 95.43
[kips]

Required shear strength
Vu
 = 
 = 24.17
[kips]

Bolt resistance factor-LRFD
φ
 = 0.75
AISC 14th  J3-10
φ Rn
 = 
 = 71.57
[kips]

ratio
 = 0.34
 > Vu
OK
 
 
End Plate / Girder - Bolt Shear
ratio = 24.17 / 71.57
= 0.34
PASS
Bolt group forces
shear V
 = 24.17
[kips]
axial P
 = 0.51
[kips]

Bolt shear stress
grade
 = A325-N
Fnv
 = 54.0
[ksi]
AISC 14th  Table J3.2
bolt dia db
 = 0.750
[in]
bolt area Ab
 = 0.442
[in2]

Number of bolt carried shear
ns
 = 4.0
shear plane m
 = 1

Bolt group eccentricity coefficient
Cec
 = 
 = 1.000

Required shear strength
Vu
 = 
 = 24.17
[kips]

Bolt shear strength
Rn
 = Fnv Ab ns m Cec
 = 95.43
[kips]
AISC 14th  Eq J3-1
Bolt resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq J3-1
φ Rn
 = 
 = 71.57
[kips]

ratio
 = 0.34
 > Vu
OK
 
End Plate / Girder - Slip Critical
ratio = 24.17 / 37.82
= 0.64
PASS
Bolt dia & bolt pretension
dia db
 = 3⁄4
[in]
Pretension Tb
 = 28.00
[kips]
AISC 14th  Table J3.1
Surface class
 = Class A
Slip coeff. μ
 = 0.30
AISC 14th  J3.8
Min. bolt pretension
Du
 = 1.13
Filler factor hf
 = 1.00
AISC 14th  J3.8
No of bolt row & column
nr
 = 2
nc
 = 2

No of slip plane
ns
 = 1

Bolt group eccentricity coefficient
Cec
 = 
 = 1.000

Required shear strength
Vu
 = 
 = 24.17
[kips]


Tension Reduction Factor
Bolt group tensile load
Tu
 = 
 = 0.51
[kips]

Number of bolt
nb
 = nr x nc
 = 4

Tension reduction factor
ksc
 = 1 -
Tu/Du Tb nb
 = 1.00
AISC 14th  Eq J3-5a

Slip resistance
Rn
 = ksc μ Du hf Tb ns nr nc Cec
 = 37.82
[kips]
AISC 14th  Eq J3-4
Resistance factor-LRFD
φ
 = 1.00
for standard size or SSLT hole
AISC 14th  J3.8
φ Rn
 = 
 = 37.82
[kips]

ratio
 = 0.64
 > Vu
OK
 
End Plate / Girder - Bolt Bearing on Girder
ratio = 24.17 / 71.57
= 0.34
PASS
Single Bolt Shear Strength

Bolt shear stress
bolt grade
 = A325-N
Fnv
 = 54.0
[ksi]
AISC 14th  Table J3.2
bolt dia db
 = 0.750
[in]
bolt area Ab
 = 0.442
[in2]

Single bolt shear strength
Rn-bolt
 = Fnv Ab
 = 23.86
[kips]
AISC 14th  Eq J3-1
Bolt Bearing/TearOut Strength on Plate


Bolt hole diameter
bolt dia db
 = 3⁄4
[in]
bolt hole dia dh
 = 13⁄16
[in]
AISC 14th  Table J3.3
Bolt spacing
spacing Ls
 = 3.000
[in]

Plate tensile strength
Fu
 = 65.0
[ksi]

Plate thickness
t
 = 0.295
[in]

Interior Bolt


Bolt hole edge clear distance
Lc
 = Ls - dh
 = 2.188
[in]

Bolt tear out/bearing strength
Rn-t&b-in
 = 1.5 Lc t Fu ≤ 3.0 db t m Fu
AISC 14th  Eq J3-6b
 = 62.92 ≤ 43.14
 = 43.14
[kips]

Bolt strength at interior
Rn-in
 = min ( Rn-t&b-in , Rn-bolt )
 = 23.86
[kips]


Number of bolt
interior nin
 = 4

Bolt bearing strength for all bolts
Rn
 = nin Rn-in
 = 95.43
[kips]

Required shear strength
Vu
 = 
 = 24.17
[kips]

Bolt resistance factor-LRFD
φ
 = 0.75
AISC 14th  J3-10
φ Rn
 = 
 = 71.57
[kips]

ratio
 = 0.34
 > Vu
OK
 
 
Bolt Tensile Prying Action on End Plate
ratio = 0.13 / 7.06
= 0.02
PASS
Bolt group forces
shear V
 = 24.17
[kips]
axial P
 = -0.51
[kips]


Single Bolt Tensile Capacity Without Considering Prying
Bolt grade
grade
 = A325-N

Nominal tensile/shear stress
Fnt
 = 90.0
[ksi]
Fnv
 = 54.0
[ksi]
AISC 14th  Table J3.2
bolt dia db
 = 0.750
[in]
bolt area Ab
 = 0.442
[in2]

Bolt group shear force
shear V
 = 24.17
[kips]
no of bolt n
 = 4

Shear stress required
frv
 = V / ( n Ab )
 = 13.68
[ksi]

Resistance factor-LRFD
φ
 = 0.75
AISC 14th  J3.7
Modified nominal tensile stress
F'nt
 = 1.3 Fnt -
Fnt/φ Fnv
frv ≤ Fnt
 = 86.61
[ksi]
AISC 14th  Eq J3-3a
Bolt norminal tensile strength
rn
 = F'nt Ab
 = 38.26
[kips]
AISC 14th  Eq J3-1
Resistance factor-LRFD
φ
 = 0.75
AISC 14th  J3.6
Single bolt tensile capacity
φ rn
 = 
 = 28.70
[kips]


Single Bolt Tensile Capacity After Considering Prying
End plate
width w
 = 6.750
[in]
bolt gage g
 = 4.000
[in]

web tw
 = 0.375
[in]


Dist from bolt center to plate edge
a
 = 0.5 (w - g)
 = 1.375
[in]

a'
 = a + 0.5 db ≤ (1.25 b + 0.5 db )
 = 1.750
[in]
AISC 14th  Eq 9-27

Bolt hole diameter
bolt dia db
 = 0.750
[in]
bolt hole dia dh
 = 0.813
[in]
AISC 14th  B4.3b
Dist from bolt center to face of web
b
 = 0.5(g - tw )
 = 1.813
[in]

b'
 = b - 0.5 db
 = 1.438
[in]
AISC 14th  Eq 9-21

Bolt pitch spacing
sv
 = 3.000

Bolt tributary length
p
 = sv     p ≤ 2b  and p ≤ sv
 = 2.875
[in]
AISC 14th  Page 9-11

ρ
 = b' / a'
 = 0.821
AISC 14th  Eq 9-26
δ
 = 1 - dh / p
 = 0.717
AISC 14th  Eq 9-24
Tensile capacity per bolt before considering prying
B
 = from calc shown in above section
 = 28.70
[kips]

Resistance factor-LRFD
φ
 = 0.90
AISC 14th  Page 9-10
End plate thickness
t
 = 0.375
[in]
tensile Fu
 = 65.0
[ksi]

Plate thickness req'd to develop bolt tensile capacity without prying
tc
 = (
4 B b'/φ p Fu
)0.5
 = 0.990
[in]
AISC 14th  Eq 9-30a
α'
 = 
1/δ (1 + ρ )
[ (
tc/t
)2 - 1 ]
 = 4.574
AISC 14th  Eq 9-35
when  α' > 1
Q
 = (
t/tc
)2 (1 + δ )
 = 0.246
AISC 14th  Eq 9-34
 
Bolt tensile force per bolt in demand
T
 = from calc shown below
 = 0.13
[kips]

 
Tensile strength per bolt after considering prying
φ rn
 = B x Q
 = 7.06
[kips]
AISC 14th  Eq 9-31
ratio
 = 0.02
 > T
OK

Calculate Max Single Bolt Tensile Load
Bolt group force
axial P
 = 0.51
[kips]

 
Bolt number
Bolt Row nh
 = 2
Bolt Col nv
 = 2

Bolt tensile force per bolt
T
 = P / ( nv nh )
 = 0.13
[kips]

 
 
Gusset Plate to End Plate Weld Strength
ratio = 2.65 / 10.97
= 0.24
PASS
Weld Group Forces
shear V
 = 24.17
[kips]
axial P
 = -0.51
[kips]   in tension
 
Gusset-end plate fillet weld length
L
 = weld length tributary to bolt group
 = 9.108
[in]

 
Combined Weld Stress
Weld stress from axial force
fa
 = P / L
 = -0.056
[kip/in]
in tension
Weld stress from shear force
fv
 = V / L
 = 2.654
[kip/in]

Weld stress combined - max
fmax
 = ( f2a + f2v )0.5
 = 2.654
[kip/in]
AISC 14th  Eq 8-11
Weld stress load angle
θ
 = tan-1 (
fa/fv
)
 = 1.2
[°]

Fillet Weld Strength Calc
Fillet weld leg size
w
 = 5⁄16
[in]
load angle θ
 = 1.2
[°]

Electrode strength
FEXX
 = 70.0
[ksi]
strength coeff C1
 = 1.00
AISC 14th  Table 8-3
Number of weld line
n
 = 2   for double fillet

Load angle coefficient
C2
 = ( 1 + 0.5 sin1.5 θ )
 = 1.00
AISC 14th  Page 8-9
Fillet weld shear strength
Rn-w
 = 0.6 (C1 x 70 ksi) 0.707 w n C2
 = 18.587
[kip/in]
AISC 14th  Eq 8-1

Base metal - gusset plate
thickness t
 = 0.375
[in]
tensile Fu
 = 65.0
[ksi]

Base metal - gusset plate is in shear, shear rupture as per AISC 14th  Eq J4-4 is checked
AISC 14th  J2.4
Base metal shear rupture
Rn-b
 = 0.6 Fu t
 = 14.625
[kip/in]
AISC 14th  Eq J4-4

Double fillet linear shear strength
Rn
 = min ( Rn-w , Rn-b )
 = 14.625
[kip/in]
AISC 14th  Eq 9-2
Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq 8-1
φ Rn
 = 
 = 10.969
[kip/in]

ratio
 = 0.24
 > fmax
OK
 
 
 
 
Brace Force Load Case 2
Gusset plate t=0.375
P =35.00 kips (C)
ratio = 0.64
PASS
Gusset Plate - Shear Yielding
ratio = 24.17 / 102.47
= 0.24
PASS
Plate Shear Yielding Check


Plate size
width bp
 = 9.108
[in]
thickness tp
 = 0.375
[in]

Plate yield strength
Fy
 = 50.0
[ksi]

Plate gross area in shear
Agv
 = bp tp
 = 3.416
[in2]

Shear force required
Vu
 = 
 = 24.17
[kips]

Plate shear yielding strength
Rn
 = 0.6 Fy Agv
 = 102.47
[kips]
AISC 14th  Eq J4-3
Resistance factor-LRFD
φ
 = 1.00
AISC 14th  Eq J4-3
φ Rn
 = 
 = 102.47
[kips]

ratio
 = 0.24
 > Vu
OK
 
Gusset Plate - Shear Rupture
ratio = 24.17 / 99.90
= 0.24
PASS
Plate Shear Rupture Check


Plate size
width bp
 = 9.108
[in]
thickness tp
 = 0.375
[in]

Plate tensile strength
Fu
 = 65.0
[ksi]

Plate net area in shear
Anv
 = bp tp
 = 3.416
[in2]

Shear force in demand
Vu
 = 
 = 24.17
[kips]

Plate shear rupture strength
Rn
 = 0.6 Fu Anv
 = 133.20
[kips]
AISC 14th  Eq J4-4
Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq J4-4
φ Rn
 = 
 = 99.90
[kips]

ratio
 = 0.24
 > Vu
OK
 
 
End Plate - Shear Yield
ratio = 12.09 / 64.69
= 0.19
PASS
Plate Shear Yielding Check


Plate size
width bp
 = 5.750
[in]
thickness tp
 = 0.375
[in]

Plate yield strength
Fy
 = 50.0
[ksi]

Plate gross area in shear
Agv
 = bp tp
 = 2.156
[in2]

Shear force required
Vu
 = 
 = 12.09
[kips]

Plate shear yielding strength
Rn
 = 0.6 Fy Agv
 = 64.69
[kips]
AISC 14th  Eq J4-3
Resistance factor-LRFD
φ
 = 1.00
AISC 14th  Eq J4-3
φ Rn
 = 
 = 64.69
[kips]

ratio
 = 0.19
 > Vu
OK
 
End Plate - Shear Rupture
ratio = 12.09 / 43.88
= 0.28
PASS
Plate Shear Rupture Check


Bolt hole diameter
bolt dia db
 = 3⁄4
[in]
bolt hole dia dh
 = 7⁄8
[in]
AISC 14th  B4.3b
Number of bolt
n
 = 2

Plate size
width bp
 = 5.750
[in]
thickness tp
 = 0.375
[in]

Plate tensile strength
Fu
 = 65.0
[ksi]

Plate net area in shear
Anv
 = ( bp - n dh ) tp
 = 1.500
[in2]

Shear force required
Vu
 = 
 = 12.09
[kips]

Plate shear rupture strength
Rn
 = 0.6 Fu Anv
 = 58.50
[kips]
AISC 14th  Eq J4-4
Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq J4-4
φ Rn
 = 
 = 43.88
[kips]

ratio
 = 0.28
 > Vu
OK
 
End Plate - Block Shear - Center Strip
ratio = 24.17 / 124.31
= 0.19
PASS
Plate Block Shear - Center Strip


Bolt hole diameter
bolt dia db
 = 3⁄4
[in]
bolt hole dia dh
 = 7⁄8
[in]
AISC 14th  B4.3b
Plate thickness
tp
 = 0.375
[in]

Plate strength
Fy
 = 50.0
[ksi]
Fu
 = 65.0
[ksi]

Bolt no in ver & hor dir
nv
 = 2
nh
 = 2

Bolt spacing in ver & hor dir
sv
 = 4.000
[in]
sh
 = 3.000
[in]

Bolt edge dist in ver & hor dir
ev
 = 1.375
[in]
eh
 = 1.375
[in]


Gross area subject to shear
Agv
 = [ (nh - 1) sh + eh ] tp x 2
 = 3.281
[in2]

Net area subject to shear
Anv
 = Agv - [(nh - 1)+ 0.5] dh tp x2
 = 2.297
[in2]

Net area subject to tension
when sheared out by center strip
Ant
 = ( nv - 1) ( sv - dh ) tp
 = 1.172
[in2]


Block shear strength required
Vu
 = 
 = 24.17
[kips]

Uniform tension stress factor
Ubs
 = 1.00
AISC 14th  Fig C-J4.2
Bolt shear resistance provided
Rn
 = min (0.6Fu Anv , 0.6Fy Agv ) +
 = 165.75
[kips]
AISC 14th  Eq J4-5
Ubs Fu Ant

Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq J4-5
φ Rn
 = 
 = 124.31
[kips]

ratio
 = 0.19
 > Vu
OK
 
End Plate - Block Shear - 2-Side Strip
ratio = 24.17 / 101.46
= 0.24
PASS
Plate Block Shear - 2 Side Strips


Bolt hole diameter
bolt dia db
 = 3⁄4
[in]
bolt hole dia dh
 = 7⁄8
[in]
AISC 14th  B4.3b
Plate thickness
tp
 = 0.375
[in]

Plate strength
Fy
 = 50.0
[ksi]
Fu
 = 65.0
[ksi]

Bolt no in ver & hor dir
nv
 = 2
nh
 = 2

Bolt spacing in ver & hor dir
sv
 = 4.000
[in]
sh
 = 3.000
[in]

Bolt edge dist in ver & hor dir
ev
 = 1.375
[in]
eh
 = 1.375
[in]


Gross area subject to shear
Agv
 = [ (nh - 1) sh + eh ] tp x 2
 = 3.281
[in2]

Net area subject to shear
Anv
 = Agv - [(nh - 1)+ 0.5] dh tp x2
 = 2.297
[in2]

Net area subject to tension
when sheared out by 2 side strips
Ant
 = ( ev - 0.5 dh ) tp x 2
 = 0.703
[in2]


Block shear strength required
Vu
 = 
 = 24.17
[kips]

Uniform tension stress factor
Ubs
 = 1.00
AISC 14th  Fig C-J4.2
Bolt shear resistance provided
Rn
 = min (0.6Fu Anv , 0.6Fy Agv ) +
 = 135.28
[kips]
AISC 14th  Eq J4-5
Ubs Fu Ant

Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq J4-5
φ Rn
 = 
 = 101.46
[kips]

ratio
 = 0.24
 > Vu
OK
 
End Plate - Bolt Bearing on End Plate
ratio = 24.17 / 71.57
= 0.34
PASS
Single Bolt Shear Strength

Bolt shear stress
bolt grade
 = A325-N
Fnv
 = 54.0
[ksi]
AISC 14th  Table J3.2
bolt dia db
 = 0.750
[in]
bolt area Ab
 = 0.442
[in2]

Single bolt shear strength
Rn-bolt
 = Fnv Ab
 = 23.86
[kips]
AISC 14th  Eq J3-1
Bolt Bearing/TearOut Strength on Plate


Bolt hole diameter
bolt dia db
 = 3⁄4
[in]
bolt hole dia dh
 = 13⁄16
[in]
AISC 14th  Table J3.3
Bolt spacing & edge distance
spacing Ls
 = 3.000
[in]
edge distance Le
 = 1.375
[in]

Plate tensile strength
Fu
 = 65.0
[ksi]

Plate thickness
t
 = 0.375
[in]

Interior Bolt


Bolt hole edge clear distance
Lc
 = Ls - dh
 = 2.188
[in]

Bolt tear out/bearing strength
Rn-t&b-in
 = 1.5 Lc t Fu ≤ 3.0 db t Fu
AISC 14th  Eq J3-6b
 = 79.98 ≤ 54.84
 = 54.84
[kips]

Bolt strength at interior
Rn-in
 = min ( Rn-t&b-in , Rn-bolt )
 = 23.86
[kips]

Edge Bolt


Bolt hole edge clear distance
Lc
 = Le - dh / 2
 = 0.969
[in]

Bolt tear out/bearing strength
Rn-t&b-ed
 = 1.5 Lc t Fu ≤ 3.0 db t Fu
AISC 14th  Eq J3-6b
 = 35.42 ≤ 54.84
 = 35.42
[kips]

Bolt strength at edge
Rn-ed
 = min ( Rn-t&b-ed , Rn-bolt )
 = 23.86
[kips]


Number of bolt
interior nin
 = 2
edge ned
 = 2

Bolt bearing strength for all bolts
Rn
 = nin Rn-in + ned Rn-ed
 = 95.43
[kips]

Required shear strength
Vu
 = 
 = 24.17
[kips]

Bolt resistance factor-LRFD
φ
 = 0.75
AISC 14th  J3-10
φ Rn
 = 
 = 71.57
[kips]

ratio
 = 0.34
 > Vu
OK
 
 
End Plate / Girder - Bolt Shear
ratio = 24.17 / 71.57
= 0.34
PASS
Bolt shear stress
bolt grade
 = A325-N
Fnv
 = 54.0
[ksi]
AISC 14th  Table J3.2
bolt dia db
 = 0.750
[in]
bolt area Ab
 = 0.442
[in2]

Number of bolt carried shear
ns
 = 4.0
shear plane m
 = 1

Bolt group eccentricity coefficient
Cec
 = 
 = 1.000

Required shear strength
Vu
 = 
 = 24.17
[kips]

Bolt shear strength
Rn
 = Fnv Ab ns m Cec
 = 95.43
[kips]
AISC 14th  Eq J3-1
Bolt resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq J3-1
φ Rn
 = 
 = 71.57
[kips]

ratio
 = 0.34
 > Vu
OK
 
End Plate / Girder - Slip Critical
ratio = 24.17 / 37.97
= 0.64
PASS
Bolt dia & bolt pretension
dia db
 = 3⁄4
[in]
Pretension Tb
 = 28.00
[kips]
AISC 14th  Table J3.1
Surface class
 = Class A
Slip coeff. μ
 = 0.30
AISC 14th  J3.8
Min. bolt pretension
Du
 = 1.13
Filler factor hf
 = 1.00
AISC 14th  J3.8
No of bolt row & column
nr
 = 2
nc
 = 2

No of slip plane
ns
 = 1

Bolt group eccentricity coefficient
Cec
 = 
 = 1.000

Required shear strength
Vu
 = 
 = 24.17
[kips]

Slip resistance
Rn
 = μ Du hf Tb ns nr nc Cec
 = 37.97
[kips]
AISC 14th  Eq J3-4
Resistance factor-LRFD
φ
 = 1.00
for standard size or SSLT hole
AISC 14th  J3.8
φ Rn
 = 
 = 37.97
[kips]

ratio
 = 0.64
 > Vu
OK
 
End Plate / Girder - Bolt Bearing on Girder
ratio = 24.17 / 71.57
= 0.34
PASS
Single Bolt Shear Strength

Bolt shear stress
bolt grade
 = A325-N
Fnv
 = 54.0
[ksi]
AISC 14th  Table J3.2
bolt dia db
 = 0.750
[in]
bolt area Ab
 = 0.442
[in2]

Single bolt shear strength
Rn-bolt
 = Fnv Ab
 = 23.86
[kips]
AISC 14th  Eq J3-1
Bolt Bearing/TearOut Strength on Plate


Bolt hole diameter
bolt dia db
 = 3⁄4
[in]
bolt hole dia dh
 = 13⁄16
[in]
AISC 14th  Table J3.3
Bolt spacing
spacing Ls
 = 3.000
[in]

Plate tensile strength
Fu
 = 65.0
[ksi]

Plate thickness
t
 = 0.295
[in]

Interior Bolt


Bolt hole edge clear distance
Lc
 = Ls - dh
 = 2.188
[in]

Bolt tear out/bearing strength
Rn-t&b-in
 = 1.5 Lc t Fu ≤ 3.0 db t m Fu
AISC 14th  Eq J3-6b
 = 62.92 ≤ 43.14
 = 43.14
[kips]

Bolt strength at interior
Rn-in
 = min ( Rn-t&b-in , Rn-bolt )
 = 23.86
[kips]


Number of bolt
interior nin
 = 4

Bolt bearing strength for all bolts
Rn
 = nin Rn-in
 = 95.43
[kips]

Required shear strength
Vu
 = 
 = 24.17
[kips]

Bolt resistance factor-LRFD
φ
 = 0.75
AISC 14th  J3-10
φ Rn
 = 
 = 71.57
[kips]

ratio
 = 0.34
 > Vu
OK
 
 
Gusset Plate to End Plate Weld Strength
ratio = 2.65 / 10.97
= 0.24
PASS
Weld Group Forces
shear V
 = 24.17
[kips]
axial P
 = 0.51
[kips]   in compression
 
Gusset-end plate fillet weld length
L
 = weld length tributary to bolt group
 = 9.108
[in]

 
Combined Weld Stress
Weld stress from axial force
fa
 = P / L
 = 0.000
[kip/in]
in compression
Weld stress from shear force
fv
 = V / L
 = 2.654
[kip/in]

Weld stress combined - max
fmax
 = fv
 = 2.654
[kip/in]
AISC 14th  Eq 8-11
Weld stress load angle
θ
 = 
 = 0.0
[°]

Fillet Weld Strength Calc
Fillet weld leg size
w
 = 5⁄16
[in]
load angle θ
 = 0.0
[°]

Electrode strength
FEXX
 = 70.0
[ksi]
strength coeff C1
 = 1.00
AISC 14th  Table 8-3
Number of weld line
n
 = 2   for double fillet

Load angle coefficient
C2
 = ( 1 + 0.5 sin1.5 θ )
 = 1.00
AISC 14th  Page 8-9
Fillet weld shear strength
Rn-w
 = 0.6 (C1 x 70 ksi) 0.707 w n C2
 = 18.559
[kip/in]
AISC 14th  Eq 8-1

Base metal - gusset plate
thickness t
 = 0.375
[in]
tensile Fu
 = 65.0
[ksi]

Base metal - gusset plate is in shear, shear rupture as per AISC 14th  Eq J4-4 is checked
AISC 14th  J2.4
Base metal shear rupture
Rn-b
 = 0.6 Fu t
 = 14.625
[kip/in]
AISC 14th  Eq J4-4

Double fillet linear shear strength
Rn
 = min ( Rn-w , Rn-b )
 = 14.625
[kip/in]
AISC 14th  Eq 9-2
Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq 8-1
φ Rn
 = 
 = 10.969
[kip/in]

ratio
 = 0.24
 > fmax
OK
 
 
 
Right Brace - Gusset to Beam
Direct Weld Connection
Code=AISC 360-10 LRFD
 
Result Summary
geometries & weld limitations = PASS
limit states max ratio 
= 0.20
PASS
 
 
Brace Weld Limitation Checks - Gusset to Beam
PASS
Min Fillet Weld Size

Thinner part joined thickness
t
 = 
 = 0.375
[in]

Min fillet weld size allowed
wmin
 = 
 = 0.188
[in]
AISC 14th  Table J2.4
Fillet weld size provided
w
 = 
 = 0.313
[in]

 > wmin
OK
Min Fillet Weld Length

Fillet weld size provided
w
 = 
 = 0.313
[in]

Min fillet weld length allowed
Lmin
 = 4 x w
 = 1.250
[in]
AISC 14th  J2.2b
Min fillet weld length
L
 = 
 = 13.652
[in]

 > Lmin
OK
 
 
 
 
Brace Force Load Case 1
Gusset plate t=0.375
P =-35.00 kips (T)
ratio = 0.20
PASS
Gusset Plate - Shear Yielding
ratio = 24.24 / 153.59
= 0.16
PASS
Plate Shear Yielding Check


Plate size
width bp
 = 13.652
[in]
thickness tp
 = 0.375
[in]

Plate yield strength
Fy
 = 50.0
[ksi]

Plate gross area in shear
Agv
 = bp tp
 = 5.120
[in2]

Shear force required
Vu
 = 
 = 24.24
[kips]

Plate shear yielding strength
Rn
 = 0.6 Fy Agv
 = 153.59
[kips]
AISC 14th  Eq J4-3
Resistance factor-LRFD
φ
 = 1.00
AISC 14th  Eq J4-3
φ Rn
 = 
 = 153.59
[kips]

ratio
 = 0.16
 > Vu
OK
 
Gusset Plate - Shear Rupture
ratio = 24.24 / 149.75
= 0.16
PASS
Plate Shear Rupture Check


Plate size
width bp
 = 13.652
[in]
thickness tp
 = 0.375
[in]

Plate tensile strength
Fu
 = 65.0
[ksi]

Plate net area in shear
Anv
 = bp tp
 = 5.120
[in2]

Shear force in demand
Vu
 = 
 = 24.24
[kips]

Plate shear rupture strength
Rn
 = 0.6 Fu Anv
 = 199.66
[kips]
AISC 14th  Eq J4-4
Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq J4-4
φ Rn
 = 
 = 149.75
[kips]

ratio
 = 0.16
 > Vu
OK
 
 
Gusset Plate - Axial Tensile Yield
ratio = 0.58 / 230.38
= 0.00
PASS
Plate Tensile Yielding Check


Plate size
width bp
 = 13.652
[in]
thickness tp
 = 0.375
[in]

Plate yield strength
Fy
 = 50.0
[ksi]

Plate gross area in shear
Ag
 = bp tp
 = 5.120
[in2]

Tensile force required
Pu
 = 
 = 0.58
[kips]

Plate tensile yielding strength
Rn
 = Fy Ag
 = 255.98
[kips]
AISC 14th  Eq J4-1
Resistance factor-LRFD
φ
 = 0.90
AISC 14th  Eq J4-1
φ Rn
 = 
 = 230.38
[kips]

ratio
 = 0.00
 > Pu
OK
 
Gusset Plate - Axial Tensile Rupture
ratio = 0.58 / 249.58
= 0.00
PASS
Plate Tensile Rupture Check


Plate size
width bp
 = 13.652
[in]
thickness tp
 = 0.375
[in]

Plate tensile strength
Fu
 = 65.0
[ksi]

Plate net area in tension
Ant
 = bp tp
 = 5.120
[in2]

Tensile force required
Pu
 = 
 = 0.58
[kips]

Plate tensile rupture strength
Rn
 = Fu Ant
 = 332.77
[kips]
AISC 14th  Eq J4-2
Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq J4-2
φ Rn
 = 
 = 249.58
[kips]
AISC 14th  Eq J4-2
ratio
 = 0.00
 > Pu
OK
 
 
Gusset Plate - Flexural Yield Interact
ratio =
= 0.02
PASS
Gusset plate
width bp
 = 13.652
[in]
thick tp
 = 0.375
[in]

yield Fy
 = 50.0
[ksi]

Shear plate - gross area
Ag
 = bp x tp
 = 5.120
[in2]

Shear plate - plastic modulus
Zp
 = ( bp x t2p ) / 4
 = 17.473
[in3]

Flexural strength available
Mc
 = φ Fy Zp     φ=0.90
 = 65.52
[kip-ft]

Flexural strength required
Mr
 = from gusset interface forces calc
 = 0.00
[kip-ft]

 
Axial strength available
Pc
 = from axial tensile yield check
 = 230.38
[kips]

Axial strength required
Pr
 = from gusset interface forces calc
 = 0.58
[kips]

 
Shear strength available
Vc
 = from shear yielding check
 = 153.59
[kips]

Shear strength required
Vr
 = from gusset interface forces calc
 = 24.24
[kips]

 
Flexural yield interaction
ratio
 = (
Vr/Vc
)2 + (
Pr/Pc
+
Mr/Mc
)2
 = 0.02
AISC 14th  Eq 10-5
 < 1.0
OK
 
Gusset Plate - Flexural Rupture Interact
ratio =
= 0.03
PASS
Gusset plate
width bp
 = 13.652
[in]
thick tp
 = 0.375
[in]

tensile Fu
 = 65.0
[ksi]

Net area of plate
An
 = bp x tp
 = 5.120
[in2]

Plastic modulus of net section
Znet
 = ( bp x t2p ) / 4
 = 17.473
[in3]

Flexural strength available
Mc
 = φ Fu Znet     φ=0.75
 = 70.98
[kip-ft]

Flexural strength required
Mr
 = from gusset interface forces calc
 = 0.00
[kip-ft]

 
Axial strength available
Pc
 = from axial tensile rupture check
 = 249.58
[kips]

Axial strength required
Pr
 = from gusset interface forces calc
 = 0.58
[kips]

 
Shear strength available
Vc
 = from shear rupture check
 = 149.75
[kips]

Shear strength required
Vr
 = from gusset interface forces calc
 = 24.24
[kips]

 
Flexural rupture interaction
ratio
 = (
Vr/Vc
)2 + (
Pr/Pc
+
Mr/Mc
)2
 = 0.03
AISC 14th  Eq 10-5
 < 1.0
OK
 
 
Gusset to Beam Weld Strength
ratio = 1.78 / 8.78
= 0.20
PASS
Gusset to Beam Interface - Forces
shear Hb
 = 24.24
[kips]
axial Vb
 = -0.58
[kips]   in tension
moment Mb
 = 0.00
[kip-ft]

 
Gusset-beam fillet weld length
Lw
 = 
 = 13.652
[in]

Gusset to Beam Interface - Combined Weld Stress
Weld stress from axial force
fa
 = Vb / Lwb
 = -0.042
[kip/in]
in tension
Weld stress from shear force
fv
 = Hb / Lwb
 = 1.776
[kip/in]

Weld stress from moment force
fb
 = 
M/L2 / 6
 = 0.000
[kip/in]

Weld stress combined - max
fmax
 = [ (fa - fb )2 + f2v ]0.5
 = 1.776
[kip/in]
AISC 14th  Eq 8-11
Weld resultant load angle
θ
 = tan-1 [( fb - fa ) / fv ]
 = 1.4
[°]

Fillet Weld Strength Calc
Fillet weld leg size
w
 = 5⁄16
[in]
load angle θ
 = 1.4
[°]

Electrode strength
FEXX
 = 70.0
[ksi]
strength coeff C1
 = 1.00
AISC 14th  Table 8-3
Number of weld line
n
 = 2   for double fillet

Load angle coefficient
C2
 = ( 1 + 0.5 sin1.5 θ )
 = 1.00
AISC 14th  Page 8-9
Fillet weld shear strength
Rn-w
 = 0.6 (C1 x 70 ksi) 0.707 w n C2
 = 18.593
[kip/in]
AISC 14th  Eq 8-1

Base metal - gusset plate
thickness t
 = 0.375
[in]
tensile Fu
 = 65.0
[ksi]

Base metal - gusset plate is in shear, shear rupture as per AISC 14th  Eq J4-4 is checked
AISC 14th  J2.4
Base metal shear rupture
Rn-b
 = 0.6 Fu t
 = 14.625
[kip/in]
AISC 14th  Eq J4-4

Double fillet linear shear strength
Rn
 = min ( Rn-w , Rn-b )
 = 14.625
[kip/in]
AISC 14th  Eq 9-2
Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq 8-1
φ Rn
 = 
 = 10.969
[kip/in]

 
When gusset plate is directly welded to beam or column, apply 1.25 ductility factor
to allow adequate force redistribution in the weld group
AISC 14th  Page 13-11
 
Weld strength used for design after applying ductility factor
φ Rn
 = φ Rn x ( 1/1.25 )
 = 8.775
[kip/in]

ratio
 = 0.20
 > fmax
OK
 
 
 
 
Brace Force Load Case 2
Gusset plate t=0.375
P =35.00 kips (C)
ratio = 0.20
PASS
Gusset Plate - Shear Yielding
ratio = 24.24 / 153.59
= 0.16
PASS
Plate Shear Yielding Check


Plate size
width bp
 = 13.652
[in]
thickness tp
 = 0.375
[in]

Plate yield strength
Fy
 = 50.0
[ksi]

Plate gross area in shear
Agv
 = bp tp
 = 5.120
[in2]

Shear force required
Vu
 = 
 = 24.24
[kips]

Plate shear yielding strength
Rn
 = 0.6 Fy Agv
 = 153.59
[kips]
AISC 14th  Eq J4-3
Resistance factor-LRFD
φ
 = 1.00
AISC 14th  Eq J4-3
φ Rn
 = 
 = 153.59
[kips]

ratio
 = 0.16
 > Vu
OK
 
Gusset Plate - Shear Rupture
ratio = 24.24 / 149.75
= 0.16
PASS
Plate Shear Rupture Check


Plate size
width bp
 = 13.652
[in]
thickness tp
 = 0.375
[in]

Plate tensile strength
Fu
 = 65.0
[ksi]

Plate net area in shear
Anv
 = bp tp
 = 5.120
[in2]

Shear force in demand
Vu
 = 
 = 24.24
[kips]

Plate shear rupture strength
Rn
 = 0.6 Fu Anv
 = 199.66
[kips]
AISC 14th  Eq J4-4
Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq J4-4
φ Rn
 = 
 = 149.75
[kips]

ratio
 = 0.16
 > Vu
OK
 
 
Gusset Plate - Axial Yield
ratio = 0.58 / 230.38
= 0.00
PASS
Plate Tensile Yielding Check


Plate size
width bp
 = 13.652
[in]
thickness tp
 = 0.375
[in]

Plate yield strength
Fy
 = 50.0
[ksi]

Plate gross area in shear
Ag
 = bp tp
 = 5.120
[in2]

Tensile force required
Pu
 = 
 = 0.58
[kips]

Plate tensile yielding strength
Rn
 = Fy Ag
 = 255.98
[kips]
AISC 14th  Eq J4-1
Resistance factor-LRFD
φ
 = 0.90
AISC 14th  Eq J4-1
φ Rn
 = 
 = 230.38
[kips]

ratio
 = 0.00
 > Pu
OK
 
 
Gusset Plate - Flexural Yield Interact
ratio =
= 0.02
PASS
Gusset plate
width bp
 = 13.652
[in]
thick tp
 = 0.375
[in]

yield Fy
 = 50.0
[ksi]

Shear plate - gross area
Ag
 = bp x tp
 = 5.120
[in2]

Shear plate - plastic modulus
Zp
 = ( bp x t2p ) / 4
 = 17.473
[in3]

Flexural strength available
Mc
 = φ Fy Zp     φ=0.90
 = 65.52
[kip-ft]

Flexural strength required
Mr
 = from gusset interface forces calc
 = 0.00
[kip-ft]

 
Axial strength available
Pc
 = from axial tensile yield check
 = 230.38
[kips]

Axial strength required
Pr
 = from gusset interface forces calc
 = 0.58
[kips]

 
Shear strength available
Vc
 = from shear yielding check
 = 153.59
[kips]

Shear strength required
Vr
 = from gusset interface forces calc
 = 24.24
[kips]

 
Flexural yield interaction
ratio
 = (
Vr/Vc
)2 + (
Pr/Pc
+
Mr/Mc
)2
 = 0.02
AISC 14th  Eq 10-5
 < 1.0
OK
 
Gusset Plate - Flexural Rupture Interact
ratio =
= 0.03
PASS
Gusset plate
width bp
 = 13.652
[in]
thick tp
 = 0.375
[in]

tensile Fu
 = 65.0
[ksi]

Net area of plate
An
 = bp x tp
 = 5.120
[in2]

Plastic modulus of net section
Znet
 = ( bp x t2p ) / 4
 = 17.473
[in3]

Flexural strength available
Mc
 = φ Fu Znet     φ=0.75
 = 70.98
[kip-ft]

Flexural strength required
Mr
 = from gusset interface forces calc
 = 0.00
[kip-ft]

 
Shear strength available
Vc
 = from shear rupture check
 = 149.75
[kips]

Shear strength required
Vr
 = from gusset interface forces calc
 = 24.24
[kips]

 
Flexural rupture interaction
ratio
 = (
Vr/Vc
)2 + (
Mr/Mc
)2
 = 0.03
AISC 14th  Eq 10-5
 < 1.0
OK
 
 
Gusset to Beam Weld Strength
ratio = 1.78 / 8.78
= 0.20
PASS
Gusset to Beam Interface - Forces
shear Hb
 = 24.24
[kips]
axial Vb
 = 0.58
[kips]   in compression
moment Mb
 = 0.00
[kip-ft]

 
Gusset-beam fillet weld length
Lw
 = 
 = 13.652
[in]

Gusset to Beam Interface - Combined Weld Stress
Weld stress from axial force
fa
 = Vb / Lwb
 = 0.000
[kip/in]
in compression
Weld stress from shear force
fv
 = Hb / Lwb
 = 1.776
[kip/in]

Weld stress from moment force
fb
 = 
M/L2 / 6
 = 0.000
[kip/in]

Weld stress combined - max
fmax
 = fv
 = 1.776
[kip/in]
AISC 14th  Eq 8-11
Weld resultant load angle
θ
 = weld only has shear component
 = 0.0
[°]

Fillet Weld Strength Calc
Fillet weld leg size
w
 = 5⁄16
[in]
load angle θ
 = 0.0
[°]

Electrode strength
FEXX
 = 70.0
[ksi]
strength coeff C1
 = 1.00
AISC 14th  Table 8-3
Number of weld line
n
 = 2   for double fillet

Load angle coefficient
C2
 = ( 1 + 0.5 sin1.5 θ )
 = 1.00
AISC 14th  Page 8-9
Fillet weld shear strength
Rn-w
 = 0.6 (C1 x 70 ksi) 0.707 w n C2
 = 18.559
[kip/in]
AISC 14th  Eq 8-1

Base metal - gusset plate
thickness t
 = 0.375
[in]
tensile Fu
 = 65.0
[ksi]

Base metal - gusset plate is in shear, shear rupture as per AISC 14th  Eq J4-4 is checked
AISC 14th  J2.4
Base metal shear rupture
Rn-b
 = 0.6 Fu t
 = 14.625
[kip/in]
AISC 14th  Eq J4-4

Double fillet linear shear strength
Rn
 = min ( Rn-w , Rn-b )
 = 14.625
[kip/in]
AISC 14th  Eq 9-2
Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq 8-1
φ Rn
 = 
 = 10.969
[kip/in]

 
When gusset plate is directly welded to beam or column, apply 1.25 ductility factor
to allow adequate force redistribution in the weld group
AISC 14th  Page 13-11
 
Weld strength used for design after applying ductility factor
φ Rn
 = φ Rn x ( 1/1.25 )
 = 8.775
[kip/in]

ratio
 = 0.20
 > fmax
OK
 
 
Beam Web Local Yielding
ratio = 0.58 / 273.90
= 0.00
PASS
 
Concentrated force from gusset
Pu
 = 
 = 0.58
[kips]

Beam section
d
 = 12.100
[in]
tf
 = 0.575
[in]

tw
 = 0.335
[in]
k
 = 1.080
[in]

yield Fy
 = 50.0
[ksi]


Length of bearing
lb
 = Gusset/Beam interface length
 = 13.652
[in]

Gusset plate corner clip
clip
 = from user input
 = 0.750
[in]

Distance from normal force applied point to member end
lN
 = 0.5 lb + clip
 = 7.576
[in]

 
when lN  ≤ d , use AISC 14th  Eq J10-3
AISC 14th  Eq J10-3
 
Beam web local yielding strength
Rn
 = Fy tw ( 2.5 k + lb )
 = 273.90
[kips]
AISC 14th  Eq J10-3
Resistance factor-LRFD
φ
 = 1.00
φ Rn
 = 
 = 273.90
[kips]

ratio
 = 0.00
 > Pu
OK
 
Beam Web Local Crippling
ratio = 0.58 / 266.12
= 0.00
PASS
 
Concentrated force from gusset
Pu
 = 
 = 0.58
[kips]

Beam section
d
 = 12.100
[in]
tf
 = 0.575
[in]

tw
 = 0.335
[in]
k
 = 1.080
[in]

yield Fy
 = 50.0
[ksi]
E
 = 29000
[ksi]


Length of bearing
lb
 = Gusset/Beam interface length
 = 13.652
[in]

Gusset plate corner clip
clip
 = from user input
 = 0.750
[in]

Distance from normal force applied point to member end
lN
 = 0.5 lb + clip
 = 7.576
[in]

 
when lN  ≥ d/2 , use Eq J10-4
AISC 14th  Eq J10-4
Beam web local crippling strength
Rn
 = 0.8 t2w [1+3
lb/d
(
tw/tf
)1.5 ] x
 = 354.83
[kips]
AISC 14th  Eq J10-4
(
E Fy tf/tw
)0.5

Resistance factor-LRFD
φ
 = 0.75
AISC 14th  J10.3
φRn
 = 
 = 266.12
[kips]

ratio
 = 0.00
 > Pu
OK
 
 
 
Left Brace - Brace to Gusset
Sect=WT4X12
PLC1 =35.00 kips (C)
PLC2 =-35.00 kips (T)
Code=AISC 360-10 LRFD
 
Result Summary
geometries & weld limitations = PASS
limit states max ratio 
= 0.92
PASS
 
 
Geometry Restriction Checks - WT Flange to Gusset
PASS
Min Bolt Edge Distance - WT Flange to Gusset

Bolt diameter
db
 = 
 = 0.750
[in]

Min edge distance allowed
Le-min
 = 
 = 1.000
[in]
AISC 14th  Table J3.4
Min edge distance in WT Flange to Gusset
Le
 = 
 = 1.250
[in]

 > Le-min
OK
Min Bolt Spacing - WT Flange to Gusset

Bolt diameter
db
 = 
 = 0.750
[in]

Min bolt spacing allowed
Ls-min
 = 2.667 db
 = 2.000
[in]
AISC 14th  J3.3
Min Bolt spacing in WT Flange to Gusset
Ls
 = 
 = 3.000
[in]

 > Ls-min
OK
 
 
 
Brace Force Load Case 1
Sect=WT4X12
P =35.00 kips (C)
ratio = 0.92
PASS
WT Brace - Bolt Shear
ratio = 35.00 / 71.57
= 0.49
PASS
Bolt shear stress
bolt grade
 = A325-N
Fnv
 = 54.0
[ksi]
AISC 14th  Table J3.2
bolt dia db
 = 0.750
[in]
bolt area Ab
 = 0.442
[in2]

Number of bolt carried shear
ns
 = 4.0
shear plane m
 = 1

Bolt group eccentricity coefficient
Cec
 = 
 = 1.000

Required shear strength
Vu
 = 
 = 35.00
[kips]

Bolt shear strength
Rn
 = Fnv Ab ns m Cec
 = 95.43
[kips]
AISC 14th  Eq J3-1
Bolt resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq J3-1
φ Rn
 = 
 = 71.57
[kips]

ratio
 = 0.49
 > Vu
OK
 
WT Brace - Slip Critical - WT Flange/Gusset Plate
ratio = 35.00 / 37.97
= 0.92
PASS
Bolt dia & bolt pretension
dia db
 = 3⁄4
[in]
Pretension Tb
 = 28.00
[kips]
AISC 14th  Table J3.1
Surface class
 = Class A
Slip coeff. μ
 = 0.30
AISC 14th  J3.8
Min. bolt pretension
Du
 = 1.13
Filler factor hf
 = 1.00
AISC 14th  J3.8
No of bolt row & column
nr
 = 2
nc
 = 2

No of slip plane
ns
 = 1

Bolt group eccentricity coefficient
Cec
 = 
 = 1.000

Required shear strength
Vu
 = 
 = 35.00
[kips]

Slip resistance
Rn
 = μ Du hf Tb ns nr nc Cec
 = 37.97
[kips]
AISC 14th  Eq J3-4
Resistance factor-LRFD
φ
 = 1.00
for standard size or SSLT hole
AISC 14th  J3.8
φ Rn
 = 
 = 37.97
[kips]

ratio
 = 0.92
 > Vu
OK
 
WT Brace - Bolt Bearing on WT Flange
ratio = 35.00 / 71.57
= 0.49
PASS
Single Bolt Shear Strength

Bolt shear stress
bolt grade
 = A325-N
Fnv
 = 54.0
[ksi]
AISC 14th  Table J3.2
bolt dia db
 = 0.750
[in]
bolt area Ab
 = 0.442
[in2]

Single bolt shear strength
Rn-bolt
 = Fnv Ab
 = 23.86
[kips]
AISC 14th  Eq J3-1
Bolt Bearing/TearOut Strength on Plate


Bolt hole diameter
bolt dia db
 = 3⁄4
[in]
bolt hole dia dh
 = 13⁄16
[in]
AISC 14th  Table J3.3
Bolt spacing
spacing Ls
 = 3.000
[in]

Plate tensile strength
Fu
 = 65.0
[ksi]

Plate thickness
t
 = 0.400
[in]

Interior Bolt


Bolt hole edge clear distance
Lc
 = Ls - dh
 = 2.188
[in]

Bolt tear out/bearing strength
Rn-t&b-in
 = 1.5 Lc t Fu ≤ 3.0 db t m Fu
AISC 14th  Eq J3-6b
 = 85.31 ≤ 58.50
 = 58.50
[kips]

Bolt strength at interior
Rn-in
 = min ( Rn-t&b-in , Rn-bolt )
 = 23.86
[kips]


Number of bolt
interior nin
 = 4

Bolt bearing strength for all bolts
Rn
 = nin Rn-in
 = 95.43
[kips]

Required shear strength
Vu
 = 
 = 35.00
[kips]

Bolt resistance factor-LRFD
φ
 = 0.75
AISC 14th  J3-10
φ Rn
 = 
 = 71.57
[kips]

ratio
 = 0.49
 > Vu
OK
 
WT Brace - Bolt Bearing on Gusset Plate
ratio = 35.00 / 71.57
= 0.49
PASS
Single Bolt Shear Strength

Bolt shear stress
bolt grade
 = A325-N
Fnv
 = 54.0
[ksi]
AISC 14th  Table J3.2
bolt dia db
 = 0.750
[in]
bolt area Ab
 = 0.442
[in2]

Single bolt shear strength
Rn-bolt
 = Fnv Ab
 = 23.86
[kips]
AISC 14th  Eq J3-1
Bolt Bearing/TearOut Strength on Plate


Bolt hole diameter
bolt dia db
 = 3⁄4
[in]
bolt hole dia dh
 = 13⁄16
[in]
AISC 14th  Table J3.3
Bolt spacing
spacing Ls
 = 3.000
[in]

Plate tensile strength
Fu
 = 65.0
[ksi]

Plate thickness
t
 = 0.375
[in]

Interior Bolt


Bolt hole edge clear distance
Lc
 = Ls - dh
 = 2.188
[in]

Bolt tear out/bearing strength
Rn-t&b-in
 = 1.5 Lc t Fu ≤ 3.0 db t m Fu
AISC 14th  Eq J3-6b
 = 79.98 ≤ 54.84
 = 54.84
[kips]

Bolt strength at interior
Rn-in
 = min ( Rn-t&b-in , Rn-bolt )
 = 23.86
[kips]


Number of bolt
interior nin
 = 4

Bolt bearing strength for all bolts
Rn
 = nin Rn-in
 = 95.43
[kips]

Required shear strength
Vu
 = 
 = 35.00
[kips]

Bolt resistance factor-LRFD
φ
 = 0.75
AISC 14th  J3-10
φ Rn
 = 
 = 71.57
[kips]

ratio
 = 0.49
 > Vu
OK
 
 
Gusset Plate - Compression (Whitmore)
ratio = 35.00 / 104.32
= 0.34
PASS
Plate Compression Check


Plate size
width bp
 = 7.464
[in]
thickness tp
 = 0.375
[in]

Fy
 = 50.0
[ksi]
E
 = 29000
[ksi]

Plate gross area in compression
Ag
 = bp tp
 = 2.799
[in2]


Plate radius of gyration
r
 = tp / √12
 = 0.108
[in]

Plate effective length factor
K
 = 
 = 0.50
Plate unbraced length
Lu
 = 
 = 10.992
[in]

Plate slenderness
KL/r
 = 0.50 x Lu  / r
 = 50.77


when  
KL/r
  >  25 , use Chapter E
AISC 14th  J4.4 (b)
Elastic buckling stress
Fe
 = 
π2 E/( KL/r )2
 = 111.04
[ksi]
AISC 14th  Eq E3-4
when  
KL/r
  ≤ 4.71 (
E/Fy
) 0.5 = 113.43
AISC 14th  E3 (a)
Critical stress
Fcr
 = 0.658 ( Fy / Fe )   Fy
 = 41.41
[ksi]
AISC 14th  Eq E3-2

Plate compression required
Pu
 = 
 = 35.00
[kips]

Plate compression provided
Rn
 = Fcr x Ag
 = 115.91
[kips]
AISC 14th  Eq E3-1
Bolt resistance factor-LRFD
φ
 = 0.90
AISC 14th  E1
φ Rn
 = 
 = 104.32
[kips]

ratio
 = 0.34
 > Pu
OK
 
 
 
Brace Force Load Case 2
Sect=WT4X12
P =-35.00 kips (T)
ratio = 0.92
PASS
WT Shape Brace - Tensile Yield
ratio = 35.00 / 159.30
= 0.22
PASS
Gross area subject to tension
Ag
 = 
 = 3.540
[in2]

Steel yield strength
Fy
 = 
 = 50.0
[ksi]

Tensile force required
Pu
 = 
 = 35.00
[kips]

Tensile yielding strength
Rn
 = Fy Ag
 = 177.00
[kips]
AISC 14th  Eq D2-1
Resistance factor-LRFD
φ
 = 0.90
AISC 14th  D2 (a)
φ Rn
 = 
 = 159.30
[kips]
AISC 14th  Eq D2-1
ratio
 = 0.22
 > Pu
OK
 
WT Shape Brace - Tensile Rupture
ratio = 35.00 / 106.38
= 0.33
PASS
Section gross area
Ag
 = WT4X12
 = 3.540
[in2]

Bolt hole diameter
bolt dia db
 = 3⁄4
[in]
bolt hole dia dh
 = 7⁄8
[in]
AISC 14th  B4.3b
Number of bolt row
nv
 = 2
flange tf
 = 0.400
[in]

Tensile net area
An
 = Ag - nv dh tf
 = 2.840
[in2]


No of bolt column
nh
 = 2
bolt space sh
 = 3.000
[in]

Length of connection
L
 = ( nh -1 ) sh
 = 3.000
[in]

Eccentricity of connection
x
 = from sect WT4X12
 = 0.695
[in]

Shear lag factor
U
 = 1 - x / L
 = 0.768
AISC 14th  Table D3.1

Tensile force required
Pu
 = 
 = 35.00
[kips]

Tensile effective net area
Ae
 = An U
 = 2.182
[in2]

Plate tensile strength
Fu
 = 
 = 65.0
[ksi]

Tensile rupture strength
Rn
 = Fu Ae
 = 141.83
[kips]
AISC 14th  Eq D2-2
Resistance factor-LRFD
φ
 = 0.75
AISC 14th  D2 (b)
φ Rn
 = 
 = 106.38
[kips]
AISC 14th  Eq D2-2
ratio
 = 0.33
 > Pu
OK
 
 
WT Brace - Bolt Shear
ratio = 35.00 / 71.57
= 0.49
PASS
Bolt shear stress
bolt grade
 = A325-N
Fnv
 = 54.0
[ksi]
AISC 14th  Table J3.2
bolt dia db
 = 0.750
[in]
bolt area Ab
 = 0.442
[in2]

Number of bolt carried shear
ns
 = 4.0
shear plane m
 = 1

Bolt group eccentricity coefficient
Cec
 = 
 = 1.000

Required shear strength
Vu
 = 
 = 35.00
[kips]

Bolt shear strength
Rn
 = Fnv Ab ns m Cec
 = 95.43
[kips]
AISC 14th  Eq J3-1
Bolt resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq J3-1
φ Rn
 = 
 = 71.57
[kips]

ratio
 = 0.49
 > Vu
OK
 
WT Brace - Slip Critical - WT Flange/Gusset Plate
ratio = 35.00 / 37.97
= 0.92
PASS
Bolt dia & bolt pretension
dia db
 = 3⁄4
[in]
Pretension Tb
 = 28.00
[kips]
AISC 14th  Table J3.1
Surface class
 = Class A
Slip coeff. μ
 = 0.30
AISC 14th  J3.8
Min. bolt pretension
Du
 = 1.13
Filler factor hf
 = 1.00
AISC 14th  J3.8
No of bolt row & column
nr
 = 2
nc
 = 2

No of slip plane
ns
 = 1

Bolt group eccentricity coefficient
Cec
 = 
 = 1.000

Required shear strength
Vu
 = 
 = 35.00
[kips]

Slip resistance
Rn
 = μ Du hf Tb ns nr nc Cec
 = 37.97
[kips]
AISC 14th  Eq J3-4
Resistance factor-LRFD
φ
 = 1.00
for standard size or SSLT hole
AISC 14th  J3.8
φ Rn
 = 
 = 37.97
[kips]

ratio
 = 0.92
 > Vu
OK
 
WT Brace - Bolt Bearing on WT Flange
ratio = 35.00 / 71.57
= 0.49
PASS
Single Bolt Shear Strength

Bolt shear stress
bolt grade
 = A325-N
Fnv
 = 54.0
[ksi]
AISC 14th  Table J3.2
bolt dia db
 = 0.750
[in]
bolt area Ab
 = 0.442
[in2]

Single bolt shear strength
Rn-bolt
 = Fnv Ab
 = 23.86
[kips]
AISC 14th  Eq J3-1
Bolt Bearing/TearOut Strength on Plate


Bolt hole diameter
bolt dia db
 = 3⁄4
[in]
bolt hole dia dh
 = 13⁄16
[in]
AISC 14th  Table J3.3
Bolt spacing & edge distance
spacing Ls
 = 3.000
[in]
edge distance Le
 = 1.375
[in]

Plate tensile strength
Fu
 = 65.0
[ksi]

Plate thickness
t
 = 0.400
[in]

Interior Bolt


Bolt hole edge clear distance
Lc
 = Ls - dh
 = 2.188
[in]

Bolt tear out/bearing strength
Rn-t&b-in
 = 1.5 Lc t Fu ≤ 3.0 db t Fu
AISC 14th  Eq J3-6b
 = 85.31 ≤ 58.50
 = 58.50
[kips]

Bolt strength at interior
Rn-in
 = min ( Rn-t&b-in , Rn-bolt )
 = 23.86
[kips]

Edge Bolt


Bolt hole edge clear distance
Lc
 = Le - dh / 2
 = 0.969
[in]

Bolt tear out/bearing strength
Rn-t&b-ed
 = 1.5 Lc t Fu ≤ 3.0 db t Fu
AISC 14th  Eq J3-6b
 = 37.78 ≤ 58.50
 = 37.78
[kips]

Bolt strength at edge
Rn-ed
 = min ( Rn-t&b-ed , Rn-bolt )
 = 23.86
[kips]


Number of bolt
interior nin
 = 2
edge ned
 = 2

Bolt bearing strength for all bolts
Rn
 = nin Rn-in + ned Rn-ed
 = 95.43
[kips]

Required shear strength
Vu
 = 
 = 35.00
[kips]

Bolt resistance factor-LRFD
φ
 = 0.75
AISC 14th  J3-10
φ Rn
 = 
 = 71.57
[kips]

ratio
 = 0.49
 > Vu
OK
 
WT Brace - Bolt Bearing on Gusset Plate
ratio = 35.00 / 71.57
= 0.49
PASS
Single Bolt Shear Strength

Bolt shear stress
bolt grade
 = A325-N
Fnv
 = 54.0
[ksi]
AISC 14th  Table J3.2
bolt dia db
 = 0.750
[in]
bolt area Ab
 = 0.442
[in2]

Single bolt shear strength
Rn-bolt
 = Fnv Ab
 = 23.86
[kips]
AISC 14th  Eq J3-1
Bolt Bearing/TearOut Strength on Plate


Bolt hole diameter
bolt dia db
 = 3⁄4
[in]
bolt hole dia dh
 = 13⁄16
[in]
AISC 14th  Table J3.3
Bolt spacing & edge distance
spacing Ls
 = 3.000
[in]
edge distance Le
 = 1.625
[in]

Plate tensile strength
Fu
 = 65.0
[ksi]

Plate thickness
t
 = 0.375
[in]

Interior Bolt


Bolt hole edge clear distance
Lc
 = Ls - dh
 = 2.188
[in]

Bolt tear out/bearing strength
Rn-t&b-in
 = 1.5 Lc t Fu ≤ 3.0 db t Fu
AISC 14th  Eq J3-6b
 = 79.98 ≤ 54.84
 = 54.84
[kips]

Bolt strength at interior
Rn-in
 = min ( Rn-t&b-in , Rn-bolt )
 = 23.86
[kips]

Edge Bolt


Bolt hole edge clear distance
Lc
 = Le - dh / 2
 = 1.219
[in]

Bolt tear out/bearing strength
Rn-t&b-ed
 = 1.5 Lc t Fu ≤ 3.0 db t Fu
AISC 14th  Eq J3-6b
 = 44.56 ≤ 54.84
 = 44.56
[kips]

Bolt strength at edge
Rn-ed
 = min ( Rn-t&b-ed , Rn-bolt )
 = 23.86
[kips]


Number of bolt
interior nin
 = 2
edge ned
 = 2

Bolt bearing strength for all bolts
Rn
 = nin Rn-in + ned Rn-ed
 = 95.43
[kips]

Required shear strength
Vu
 = 
 = 35.00
[kips]

Bolt resistance factor-LRFD
φ
 = 0.75
AISC 14th  J3-10
φ Rn
 = 
 = 71.57
[kips]

ratio
 = 0.49
 > Vu
OK
 
WT Brace Flange - Block Shear - 1-Side Strip
ratio = 17.50 / 51.68
= 0.34
PASS
Plate Block Shear - Side Strip


Bolt hole diameter
bolt dia db
 = 3⁄4
[in]
bolt hole dia dh
 = 7⁄8
[in]
AISC 14th  B4.3b
Plate thickness
tp
 = 0.400
[in]

Plate strength
Fy
 = 50.0
[ksi]
Fu
 = 65.0
[ksi]

Bolt no in ver & hor dir
nv
 = 1
nh
 = 2

Bolt spacing in hor dir
sh
 = 3.000
[in]

Bolt edge dist in ver & hor dir
ev
 = 1.250
[in]
eh
 = 1.375
[in]


Gross area subject to shear
Agv
 = [ (nh - 1) sh + eh ] tp
 = 1.750
[in2]

Net area subject to shear
Anv
 = Agv - [ (nh - 1) + 0.5 ] dh tp
 = 1.225
[in2]

Net area subject to tension
Ant
 = ( ev - 0.5 dh ) tp
 = 0.325
[in2]


Block shear strength required
Vu
 = 
 = 17.50
[kips]

Uniform tension stress factor
Ubs
 = 1.00
AISC 14th  Fig C-J4.2
Bolt shear resistance provided
Rn
 = min (0.6Fu Anv , 0.6Fy Agv ) +
 = 68.90
[kips]
AISC 14th  Eq J4-5
Ubs Fu Ant

Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq J4-5
φ Rn
 = 
 = 51.68
[kips]

ratio
 = 0.34
 > Vu
OK
 
 
Gusset Plate - Tensile Yield (Whitmore)
ratio = 35.00 / 125.96
= 0.28
PASS
Plate Tensile Yielding Check


Plate size
width bp
 = 7.464
[in]
thickness tp
 = 0.375
[in]

Plate yield strength
Fy
 = 50.0
[ksi]

Plate gross area in shear
Ag
 = bp tp
 = 2.799
[in2]

Tensile force required
Pu
 = 
 = 35.00
[kips]

Plate tensile yielding strength
Rn
 = Fy Ag
 = 139.95
[kips]
AISC 14th  Eq J4-1
Resistance factor-LRFD
φ
 = 0.90
AISC 14th  Eq J4-1
φ Rn
 = 
 = 125.96
[kips]

ratio
 = 0.28
 > Pu
OK
 
Gusset Plate - Tensile Rupture (Whitmore)
ratio = 35.00 / 104.46
= 0.34
PASS
Plate Tensile Rupture Check


Bolt hole diameter
bolt dia db
 = 3⁄4
[in]
bolt hole dia dh
 = 7⁄8
[in]
AISC 14th  B4.3b
Number of bolt
n
 = 2

Plate size
width bp
 = 7.464
[in]
thickness tp
 = 0.375
[in]

Plate tensile strength
Fu
 = 65.0
[ksi]

Plate net area in tension
Ant
 = ( bp - n dh ) tp
 = 2.143
[in2]

Tensile force required
Pu
 = 
 = 35.00
[kips]

Plate tensile rupture strength
Rn
 = Fu Ant
 = 139.28
[kips]
AISC 14th  Eq J4-2
Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq J4-2
φ Rn
 = 
 = 104.46
[kips]
AISC 14th  Eq J4-2
ratio
 = 0.34
 > Pu
OK
 
Gusset Plate - Block Shear - Center Strip
ratio = 35.00 / 129.80
= 0.27
PASS
Plate Block Shear - Center Strip


Bolt hole diameter
bolt dia db
 = 3⁄4
[in]
bolt hole dia dh
 = 7⁄8
[in]
AISC 14th  B4.3b
Plate thickness
tp
 = 0.375
[in]

Plate strength
Fy
 = 50.0
[ksi]
Fu
 = 65.0
[ksi]

Bolt no in ver & hor dir
nv
 = 2.0
nh
 = 2

Bolt spacing in hor dir
sh
 = 3.000
[in]
edge dist eh
 = 1.625
[in]

Width of block shear strip
Wbs
 = 4.000
[in]


Gross area subject to shear
Agv
 = [ (nh - 1) sh + eh ] tp x 2
 = 3.469
[in2]

Net area subject to shear
Anv
 = Agv - [(nh - 1)+ 0.5] dh tp x2
 = 2.484
[in2]

Net area subject to tension
when sheared out by center strip
Ant
 = [ Wbs - (nv - 1) dh ] tp
 = 1.172
[in2]


Block shear strength required
Vu
 = 
 = 35.00
[kips]

Uniform tension stress factor
Ubs
 = 1.00
AISC 14th  Fig C-J4.2
Bolt shear resistance provided
Rn
 = min (0.6Fu Anv , 0.6Fy Agv ) +
 = 173.06
[kips]
AISC 14th  Eq J4-5
Ubs Fu Ant

Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq J4-5
φ Rn
 = 
 = 129.80
[kips]

ratio
 = 0.27
 > Vu
OK
 
 
Left Brace - Gusset to Girder
End Plate Connection
Code=AISC 360-10 LRFD
 
Result Summary
geometries & weld limitations = PASS
limit states max ratio 
= 0.64
PASS
 
 
Geometry Restriction Checks - End Plate to Column Web
PASS
Min Bolt Edge Distance - End Plate to Column Web

Bolt diameter
db
 = 
 = 0.750
[in]

Min edge distance allowed
Le-min
 = 
 = 1.000
[in]
AISC 14th  Table J3.4
Min edge distance in End Plate to Column Web
Le
 = 
 = 1.375
[in]

 > Le-min
OK
Min Bolt Spacing - End Plate to Column Web

Bolt diameter
db
 = 
 = 0.750
[in]

Min bolt spacing allowed
Ls-min
 = 2.667 db
 = 2.000
[in]
AISC 14th  J3.3
Min Bolt spacing in End Plate to Column Web
Ls
 = 
 = 3.000
[in]

 > Ls-min
OK
 
Weld Limitation Checks - Gusset Plate to End Plate
PASS
Min Fillet Weld Size

Thinner part joined thickness
t
 = 
 = 0.375
[in]

Min fillet weld size allowed
wmin
 = 
 = 0.188
[in]
AISC 14th  Table J2.4
Fillet weld size provided
w
 = 
 = 0.313
[in]

 > wmin
OK
Min Fillet Weld Length

Fillet weld size provided
w
 = 
 = 0.313
[in]

Min fillet weld length allowed
Lmin
 = 4 x w
 = 1.250
[in]
AISC 14th  J2.2b
Min fillet weld length
L
 = 
 = 9.108
[in]

 > Lmin
OK
 
 
 
 
Brace Force Load Case 1
Gusset plate t=0.375
P =35.00 kips (C)
ratio = 0.64
PASS
Gusset Plate - Shear Yielding
ratio = 24.17 / 102.47
= 0.24
PASS
Plate Shear Yielding Check


Plate size
width bp
 = 9.108
[in]
thickness tp
 = 0.375
[in]

Plate yield strength
Fy
 = 50.0
[ksi]

Plate gross area in shear
Agv
 = bp tp
 = 3.416
[in2]

Shear force required
Vu
 = 
 = 24.17
[kips]

Plate shear yielding strength
Rn
 = 0.6 Fy Agv
 = 102.47
[kips]
AISC 14th  Eq J4-3
Resistance factor-LRFD
φ
 = 1.00
AISC 14th  Eq J4-3
φ Rn
 = 
 = 102.47
[kips]

ratio
 = 0.24
 > Vu
OK
 
Gusset Plate - Shear Rupture
ratio = 24.17 / 99.90
= 0.24
PASS
Plate Shear Rupture Check


Plate size
width bp
 = 9.108
[in]
thickness tp
 = 0.375
[in]

Plate tensile strength
Fu
 = 65.0
[ksi]

Plate net area in shear
Anv
 = bp tp
 = 3.416
[in2]

Shear force in demand
Vu
 = 
 = 24.17
[kips]

Plate shear rupture strength
Rn
 = 0.6 Fu Anv
 = 133.20
[kips]
AISC 14th  Eq J4-4
Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq J4-4
φ Rn
 = 
 = 99.90
[kips]

ratio
 = 0.24
 > Vu
OK
 
 
End Plate - Shear Yield
ratio = 12.09 / 64.69
= 0.19
PASS
Plate Shear Yielding Check


Plate size
width bp
 = 5.750
[in]
thickness tp
 = 0.375
[in]

Plate yield strength
Fy
 = 50.0
[ksi]

Plate gross area in shear
Agv
 = bp tp
 = 2.156
[in2]

Shear force required
Vu
 = 
 = 12.09
[kips]

Plate shear yielding strength
Rn
 = 0.6 Fy Agv
 = 64.69
[kips]
AISC 14th  Eq J4-3
Resistance factor-LRFD
φ
 = 1.00
AISC 14th  Eq J4-3
φ Rn
 = 
 = 64.69
[kips]

ratio
 = 0.19
 > Vu
OK
 
End Plate - Shear Rupture
ratio = 12.09 / 43.88
= 0.28
PASS
Plate Shear Rupture Check


Bolt hole diameter
bolt dia db
 = 3⁄4
[in]
bolt hole dia dh
 = 7⁄8
[in]
AISC 14th  B4.3b
Number of bolt
n
 = 2

Plate size
width bp
 = 5.750
[in]
thickness tp
 = 0.375
[in]

Plate tensile strength
Fu
 = 65.0
[ksi]

Plate net area in shear
Anv
 = ( bp - n dh ) tp
 = 1.500
[in2]

Shear force required
Vu
 = 
 = 12.09
[kips]

Plate shear rupture strength
Rn
 = 0.6 Fu Anv
 = 58.50
[kips]
AISC 14th  Eq J4-4
Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq J4-4
φ Rn
 = 
 = 43.88
[kips]

ratio
 = 0.28
 > Vu
OK
 
End Plate - Block Shear - Center Strip
ratio = 24.17 / 115.17
= 0.21
PASS
Plate Block Shear - Center Strip


Bolt hole diameter
bolt dia db
 = 3⁄4
[in]
bolt hole dia dh
 = 7⁄8
[in]
AISC 14th  B4.3b
Plate thickness
tp
 = 0.375
[in]

Plate strength
Fy
 = 50.0
[ksi]
Fu
 = 65.0
[ksi]

Bolt no in ver & hor dir
nv
 = 2
nh
 = 2

Bolt spacing in ver & hor dir
sv
 = 3.500
[in]
sh
 = 3.000
[in]

Bolt edge dist in ver & hor dir
ev
 = 1.375
[in]
eh
 = 1.375
[in]


Gross area subject to shear
Agv
 = [ (nh - 1) sh + eh ] tp x 2
 = 3.281
[in2]

Net area subject to shear
Anv
 = Agv - [(nh - 1)+ 0.5] dh tp x2
 = 2.297
[in2]

Net area subject to tension
when sheared out by center strip
Ant
 = ( nv - 1) ( sv - dh ) tp
 = 0.984
[in2]


Block shear strength required
Vu
 = 
 = 24.17
[kips]

Uniform tension stress factor
Ubs
 = 1.00
AISC 14th  Fig C-J4.2
Bolt shear resistance provided
Rn
 = min (0.6Fu Anv , 0.6Fy Agv ) +
 = 153.56
[kips]
AISC 14th  Eq J4-5
Ubs Fu Ant

Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq J4-5
φ Rn
 = 
 = 115.17
[kips]

ratio
 = 0.21
 > Vu
OK
 
End Plate - Block Shear - 2-Side Strip
ratio = 24.17 / 101.46
= 0.24
PASS
Plate Block Shear - 2 Side Strips


Bolt hole diameter
bolt dia db
 = 3⁄4
[in]
bolt hole dia dh
 = 7⁄8
[in]
AISC 14th  B4.3b
Plate thickness
tp
 = 0.375
[in]

Plate strength
Fy
 = 50.0
[ksi]
Fu
 = 65.0
[ksi]

Bolt no in ver & hor dir
nv
 = 2
nh
 = 2

Bolt spacing in ver & hor dir
sv
 = 3.500
[in]
sh
 = 3.000
[in]

Bolt edge dist in ver & hor dir
ev
 = 1.375
[in]
eh
 = 1.375
[in]


Gross area subject to shear
Agv
 = [ (nh - 1) sh + eh ] tp x 2
 = 3.281
[in2]

Net area subject to shear
Anv
 = Agv - [(nh - 1)+ 0.5] dh tp x2
 = 2.297
[in2]

Net area subject to tension
when sheared out by 2 side strips
Ant
 = ( ev - 0.5 dh ) tp x 2
 = 0.703
[in2]


Block shear strength required
Vu
 = 
 = 24.17
[kips]

Uniform tension stress factor
Ubs
 = 1.00
AISC 14th  Fig C-J4.2
Bolt shear resistance provided
Rn
 = min (0.6Fu Anv , 0.6Fy Agv ) +
 = 135.28
[kips]
AISC 14th  Eq J4-5
Ubs Fu Ant

Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq J4-5
φ Rn
 = 
 = 101.46
[kips]

ratio
 = 0.24
 > Vu
OK
 
End Plate - Bolt Bearing on End Plate
ratio = 24.17 / 71.57
= 0.34
PASS
Single Bolt Shear Strength

Bolt shear stress
bolt grade
 = A325-N
Fnv
 = 54.0
[ksi]
AISC 14th  Table J3.2
bolt dia db
 = 0.750
[in]
bolt area Ab
 = 0.442
[in2]

Single bolt shear strength
Rn-bolt
 = Fnv Ab
 = 23.86
[kips]
AISC 14th  Eq J3-1
Bolt Bearing/TearOut Strength on Plate


Bolt hole diameter
bolt dia db
 = 3⁄4
[in]
bolt hole dia dh
 = 13⁄16
[in]
AISC 14th  Table J3.3
Bolt spacing & edge distance
spacing Ls
 = 3.000
[in]
edge distance Le
 = 1.375
[in]

Plate tensile strength
Fu
 = 65.0
[ksi]

Plate thickness
t
 = 0.375
[in]

Interior Bolt


Bolt hole edge clear distance
Lc
 = Ls - dh
 = 2.188
[in]

Bolt tear out/bearing strength
Rn-t&b-in
 = 1.5 Lc t Fu ≤ 3.0 db t Fu
AISC 14th  Eq J3-6b
 = 79.98 ≤ 54.84
 = 54.84
[kips]

Bolt strength at interior
Rn-in
 = min ( Rn-t&b-in , Rn-bolt )
 = 23.86
[kips]

Edge Bolt


Bolt hole edge clear distance
Lc
 = Le - dh / 2
 = 0.969
[in]

Bolt tear out/bearing strength
Rn-t&b-ed
 = 1.5 Lc t Fu ≤ 3.0 db t Fu
AISC 14th  Eq J3-6b
 = 35.42 ≤ 54.84
 = 35.42
[kips]

Bolt strength at edge
Rn-ed
 = min ( Rn-t&b-ed , Rn-bolt )
 = 23.86
[kips]


Number of bolt
interior nin
 = 2
edge ned
 = 2

Bolt bearing strength for all bolts
Rn
 = nin Rn-in + ned Rn-ed
 = 95.43
[kips]

Required shear strength
Vu
 = 
 = 24.17
[kips]

Bolt resistance factor-LRFD
φ
 = 0.75
AISC 14th  J3-10
φ Rn
 = 
 = 71.57
[kips]

ratio
 = 0.34
 > Vu
OK
 
 
End Plate / Girder - Bolt Shear
ratio = 24.17 / 71.57
= 0.34
PASS
Bolt shear stress
bolt grade
 = A325-N
Fnv
 = 54.0
[ksi]
AISC 14th  Table J3.2
bolt dia db
 = 0.750
[in]
bolt area Ab
 = 0.442
[in2]

Number of bolt carried shear
ns
 = 4.0
shear plane m
 = 1

Bolt group eccentricity coefficient
Cec
 = 
 = 1.000

Required shear strength
Vu
 = 
 = 24.17
[kips]

Bolt shear strength
Rn
 = Fnv Ab ns m Cec
 = 95.43
[kips]
AISC 14th  Eq J3-1
Bolt resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq J3-1
φ Rn
 = 
 = 71.57
[kips]

ratio
 = 0.34
 > Vu
OK
 
End Plate / Girder - Slip Critical
ratio = 24.17 / 37.97
= 0.64
PASS
Bolt dia & bolt pretension
dia db
 = 3⁄4
[in]
Pretension Tb
 = 28.00
[kips]
AISC 14th  Table J3.1
Surface class
 = Class A
Slip coeff. μ
 = 0.30
AISC 14th  J3.8
Min. bolt pretension
Du
 = 1.13
Filler factor hf
 = 1.00
AISC 14th  J3.8
No of bolt row & column
nr
 = 2
nc
 = 2

No of slip plane
ns
 = 1

Bolt group eccentricity coefficient
Cec
 = 
 = 1.000

Required shear strength
Vu
 = 
 = 24.17
[kips]

Slip resistance
Rn
 = μ Du hf Tb ns nr nc Cec
 = 37.97
[kips]
AISC 14th  Eq J3-4
Resistance factor-LRFD
φ
 = 1.00
for standard size or SSLT hole
AISC 14th  J3.8
φ Rn
 = 
 = 37.97
[kips]

ratio
 = 0.64
 > Vu
OK
 
End Plate / Girder - Bolt Bearing on Girder
ratio = 24.17 / 71.57
= 0.34
PASS
Single Bolt Shear Strength

Bolt shear stress
bolt grade
 = A325-N
Fnv
 = 54.0
[ksi]
AISC 14th  Table J3.2
bolt dia db
 = 0.750
[in]
bolt area Ab
 = 0.442
[in2]

Single bolt shear strength
Rn-bolt
 = Fnv Ab
 = 23.86
[kips]
AISC 14th  Eq J3-1
Bolt Bearing/TearOut Strength on Plate


Bolt hole diameter
bolt dia db
 = 3⁄4
[in]
bolt hole dia dh
 = 13⁄16
[in]
AISC 14th  Table J3.3
Bolt spacing
spacing Ls
 = 3.000
[in]

Plate tensile strength
Fu
 = 65.0
[ksi]

Plate thickness
t
 = 0.295
[in]

Interior Bolt


Bolt hole edge clear distance
Lc
 = Ls - dh
 = 2.188
[in]

Bolt tear out/bearing strength
Rn-t&b-in
 = 1.5 Lc t Fu ≤ 3.0 db t m Fu
AISC 14th  Eq J3-6b
 = 62.92 ≤ 43.14
 = 43.14
[kips]

Bolt strength at interior
Rn-in
 = min ( Rn-t&b-in , Rn-bolt )
 = 23.86
[kips]


Number of bolt
interior nin
 = 4

Bolt bearing strength for all bolts
Rn
 = nin Rn-in
 = 95.43
[kips]

Required shear strength
Vu
 = 
 = 24.17
[kips]

Bolt resistance factor-LRFD
φ
 = 0.75
AISC 14th  J3-10
φ Rn
 = 
 = 71.57
[kips]

ratio
 = 0.34
 > Vu
OK
 
 
Gusset Plate to End Plate Weld Strength
ratio = 2.65 / 10.97
= 0.24
PASS
Weld Group Forces
shear V
 = 24.17
[kips]
axial P
 = 0.51
[kips]   in compression
 
Gusset-end plate fillet weld length
L
 = weld length tributary to bolt group
 = 9.108
[in]

 
Combined Weld Stress
Weld stress from axial force
fa
 = P / L
 = 0.000
[kip/in]
in compression
Weld stress from shear force
fv
 = V / L
 = 2.654
[kip/in]

Weld stress combined - max
fmax
 = fv
 = 2.654
[kip/in]
AISC 14th  Eq 8-11
Weld stress load angle
θ
 = 
 = 0.0
[°]

Fillet Weld Strength Calc
Fillet weld leg size
w
 = 5⁄16
[in]
load angle θ
 = 0.0
[°]

Electrode strength
FEXX
 = 70.0
[ksi]
strength coeff C1
 = 1.00
AISC 14th  Table 8-3
Number of weld line
n
 = 2   for double fillet

Load angle coefficient
C2
 = ( 1 + 0.5 sin1.5 θ )
 = 1.00
AISC 14th  Page 8-9
Fillet weld shear strength
Rn-w
 = 0.6 (C1 x 70 ksi) 0.707 w n C2
 = 18.559
[kip/in]
AISC 14th  Eq 8-1

Base metal - gusset plate
thickness t
 = 0.375
[in]
tensile Fu
 = 65.0
[ksi]

Base metal - gusset plate is in shear, shear rupture as per AISC 14th  Eq J4-4 is checked
AISC 14th  J2.4
Base metal shear rupture
Rn-b
 = 0.6 Fu t
 = 14.625
[kip/in]
AISC 14th  Eq J4-4

Double fillet linear shear strength
Rn
 = min ( Rn-w , Rn-b )
 = 14.625
[kip/in]
AISC 14th  Eq 9-2
Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq 8-1
φ Rn
 = 
 = 10.969
[kip/in]

ratio
 = 0.24
 > fmax
OK
 
 
 
 
Brace Force Load Case 2
Gusset plate t=0.375
P =-35.00 kips (T)
ratio = 0.64
PASS
Gusset Plate - Shear Yielding
ratio = 24.17 / 102.47
= 0.24
PASS
Plate Shear Yielding Check


Plate size
width bp
 = 9.108
[in]
thickness tp
 = 0.375
[in]

Plate yield strength
Fy
 = 50.0
[ksi]

Plate gross area in shear
Agv
 = bp tp
 = 3.416
[in2]

Shear force required
Vu
 = 
 = 24.17
[kips]

Plate shear yielding strength
Rn
 = 0.6 Fy Agv
 = 102.47
[kips]
AISC 14th  Eq J4-3
Resistance factor-LRFD
φ
 = 1.00
AISC 14th  Eq J4-3
φ Rn
 = 
 = 102.47
[kips]

ratio
 = 0.24
 > Vu
OK
 
Gusset Plate - Shear Rupture
ratio = 24.17 / 99.90
= 0.24
PASS
Plate Shear Rupture Check


Plate size
width bp
 = 9.108
[in]
thickness tp
 = 0.375
[in]

Plate tensile strength
Fu
 = 65.0
[ksi]

Plate net area in shear
Anv
 = bp tp
 = 3.416
[in2]

Shear force in demand
Vu
 = 
 = 24.17
[kips]

Plate shear rupture strength
Rn
 = 0.6 Fu Anv
 = 133.20
[kips]
AISC 14th  Eq J4-4
Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq J4-4
φ Rn
 = 
 = 99.90
[kips]

ratio
 = 0.24
 > Vu
OK
 
 
End Plate - Shear Yield
ratio = 12.09 / 64.69
= 0.19
PASS
Plate Shear Yielding Check


Plate size
width bp
 = 5.750
[in]
thickness tp
 = 0.375
[in]

Plate yield strength
Fy
 = 50.0
[ksi]

Plate gross area in shear
Agv
 = bp tp
 = 2.156
[in2]

Shear force required
Vu
 = 
 = 12.09
[kips]

Plate shear yielding strength
Rn
 = 0.6 Fy Agv
 = 64.69
[kips]
AISC 14th  Eq J4-3
Resistance factor-LRFD
φ
 = 1.00
AISC 14th  Eq J4-3
φ Rn
 = 
 = 64.69
[kips]

ratio
 = 0.19
 > Vu
OK
 
End Plate - Shear Rupture
ratio = 12.09 / 43.88
= 0.28
PASS
Plate Shear Rupture Check


Bolt hole diameter
bolt dia db
 = 3⁄4
[in]
bolt hole dia dh
 = 7⁄8
[in]
AISC 14th  B4.3b
Number of bolt
n
 = 2

Plate size
width bp
 = 5.750
[in]
thickness tp
 = 0.375
[in]

Plate tensile strength
Fu
 = 65.0
[ksi]

Plate net area in shear
Anv
 = ( bp - n dh ) tp
 = 1.500
[in2]

Shear force required
Vu
 = 
 = 12.09
[kips]

Plate shear rupture strength
Rn
 = 0.6 Fu Anv
 = 58.50
[kips]
AISC 14th  Eq J4-4
Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq J4-4
φ Rn
 = 
 = 43.88
[kips]

ratio
 = 0.28
 > Vu
OK
 
End Plate - Block Shear - Center Strip
ratio = 24.17 / 115.17
= 0.21
PASS
Plate Block Shear - Center Strip


Bolt hole diameter
bolt dia db
 = 3⁄4
[in]
bolt hole dia dh
 = 7⁄8
[in]
AISC 14th  B4.3b
Plate thickness
tp
 = 0.375
[in]

Plate strength
Fy
 = 50.0
[ksi]
Fu
 = 65.0
[ksi]

Bolt no in ver & hor dir
nv
 = 2
nh
 = 2

Bolt spacing in ver & hor dir
sv
 = 3.500
[in]
sh
 = 3.000
[in]

Bolt edge dist in ver & hor dir
ev
 = 1.375
[in]
eh
 = 1.375
[in]


Gross area subject to shear
Agv
 = [ (nh - 1) sh + eh ] tp x 2
 = 3.281
[in2]

Net area subject to shear
Anv
 = Agv - [(nh - 1)+ 0.5] dh tp x2
 = 2.297
[in2]

Net area subject to tension
when sheared out by center strip
Ant
 = ( nv - 1) ( sv - dh ) tp
 = 0.984
[in2]


Block shear strength required
Vu
 = 
 = 24.17
[kips]

Uniform tension stress factor
Ubs
 = 1.00
AISC 14th  Fig C-J4.2
Bolt shear resistance provided
Rn
 = min (0.6Fu Anv , 0.6Fy Agv ) +
 = 153.56
[kips]
AISC 14th  Eq J4-5
Ubs Fu Ant

Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq J4-5
φ Rn
 = 
 = 115.17
[kips]

ratio
 = 0.21
 > Vu
OK
 
End Plate - Block Shear - 2-Side Strip
ratio = 24.17 / 101.46
= 0.24
PASS
Plate Block Shear - 2 Side Strips


Bolt hole diameter
bolt dia db
 = 3⁄4
[in]
bolt hole dia dh
 = 7⁄8
[in]
AISC 14th  B4.3b
Plate thickness
tp
 = 0.375
[in]

Plate strength
Fy
 = 50.0
[ksi]
Fu
 = 65.0
[ksi]

Bolt no in ver & hor dir
nv
 = 2
nh
 = 2

Bolt spacing in ver & hor dir
sv
 = 3.500
[in]
sh
 = 3.000
[in]

Bolt edge dist in ver & hor dir
ev
 = 1.375
[in]
eh
 = 1.375
[in]


Gross area subject to shear
Agv
 = [ (nh - 1) sh + eh ] tp x 2
 = 3.281
[in2]

Net area subject to shear
Anv
 = Agv - [(nh - 1)+ 0.5] dh tp x2
 = 2.297
[in2]

Net area subject to tension
when sheared out by 2 side strips
Ant
 = ( ev - 0.5 dh ) tp x 2
 = 0.703
[in2]


Block shear strength required
Vu
 = 
 = 24.17
[kips]

Uniform tension stress factor
Ubs
 = 1.00
AISC 14th  Fig C-J4.2
Bolt shear resistance provided
Rn
 = min (0.6Fu Anv , 0.6Fy Agv ) +
 = 135.28
[kips]
AISC 14th  Eq J4-5
Ubs Fu Ant

Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq J4-5
φ Rn
 = 
 = 101.46
[kips]

ratio
 = 0.24
 > Vu
OK
 
End Plate - Bolt Bearing on End Plate
ratio = 24.17 / 71.57
= 0.34
PASS
Single Bolt Shear Strength

Bolt shear stress
bolt grade
 = A325-N
Fnv
 = 54.0
[ksi]
AISC 14th  Table J3.2
bolt dia db
 = 0.750
[in]
bolt area Ab
 = 0.442
[in2]

Single bolt shear strength
Rn-bolt
 = Fnv Ab
 = 23.86
[kips]
AISC 14th  Eq J3-1
Bolt Bearing/TearOut Strength on Plate


Bolt hole diameter
bolt dia db
 = 3⁄4
[in]
bolt hole dia dh
 = 13⁄16
[in]
AISC 14th  Table J3.3
Bolt spacing & edge distance
spacing Ls
 = 3.000
[in]
edge distance Le
 = 1.375
[in]

Plate tensile strength
Fu
 = 65.0
[ksi]

Plate thickness
t
 = 0.375
[in]

Interior Bolt


Bolt hole edge clear distance
Lc
 = Ls - dh
 = 2.188
[in]

Bolt tear out/bearing strength
Rn-t&b-in
 = 1.5 Lc t Fu ≤ 3.0 db t Fu
AISC 14th  Eq J3-6b
 = 79.98 ≤ 54.84
 = 54.84
[kips]

Bolt strength at interior
Rn-in
 = min ( Rn-t&b-in , Rn-bolt )
 = 23.86
[kips]

Edge Bolt


Bolt hole edge clear distance
Lc
 = Le - dh / 2
 = 0.969
[in]

Bolt tear out/bearing strength
Rn-t&b-ed
 = 1.5 Lc t Fu ≤ 3.0 db t Fu
AISC 14th  Eq J3-6b
 = 35.42 ≤ 54.84
 = 35.42
[kips]

Bolt strength at edge
Rn-ed
 = min ( Rn-t&b-ed , Rn-bolt )
 = 23.86
[kips]


Number of bolt
interior nin
 = 2
edge ned
 = 2

Bolt bearing strength for all bolts
Rn
 = nin Rn-in + ned Rn-ed
 = 95.43
[kips]

Required shear strength
Vu
 = 
 = 24.17
[kips]

Bolt resistance factor-LRFD
φ
 = 0.75
AISC 14th  J3-10
φ Rn
 = 
 = 71.57
[kips]

ratio
 = 0.34
 > Vu
OK
 
 
End Plate / Girder - Bolt Shear
ratio = 24.17 / 71.57
= 0.34
PASS
Bolt group forces
shear V
 = 24.17
[kips]
axial P
 = 0.51
[kips]

Bolt shear stress
grade
 = A325-N
Fnv
 = 54.0
[ksi]
AISC 14th  Table J3.2
bolt dia db
 = 0.750
[in]
bolt area Ab
 = 0.442
[in2]

Number of bolt carried shear
ns
 = 4.0
shear plane m
 = 1

Bolt group eccentricity coefficient
Cec
 = 
 = 1.000

Required shear strength
Vu
 = 
 = 24.17
[kips]

Bolt shear strength
Rn
 = Fnv Ab ns m Cec
 = 95.43
[kips]
AISC 14th  Eq J3-1
Bolt resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq J3-1
φ Rn
 = 
 = 71.57
[kips]

ratio
 = 0.34
 > Vu
OK
 
End Plate / Girder - Slip Critical
ratio = 24.17 / 37.82
= 0.64
PASS
Bolt dia & bolt pretension
dia db
 = 3⁄4
[in]
Pretension Tb
 = 28.00
[kips]
AISC 14th  Table J3.1
Surface class
 = Class A
Slip coeff. μ
 = 0.30
AISC 14th  J3.8
Min. bolt pretension
Du
 = 1.13
Filler factor hf
 = 1.00
AISC 14th  J3.8
No of bolt row & column
nr
 = 2
nc
 = 2

No of slip plane
ns
 = 1

Bolt group eccentricity coefficient
Cec
 = 
 = 1.000

Required shear strength
Vu
 = 
 = 24.17
[kips]


Tension Reduction Factor
Bolt group tensile load
Tu
 = 
 = 0.51
[kips]

Number of bolt
nb
 = nr x nc
 = 4

Tension reduction factor
ksc
 = 1 -
Tu/Du Tb nb
 = 1.00
AISC 14th  Eq J3-5a

Slip resistance
Rn
 = ksc μ Du hf Tb ns nr nc Cec
 = 37.82
[kips]
AISC 14th  Eq J3-4
Resistance factor-LRFD
φ
 = 1.00
for standard size or SSLT hole
AISC 14th  J3.8
φ Rn
 = 
 = 37.82
[kips]

ratio
 = 0.64
 > Vu
OK
 
End Plate / Girder - Bolt Bearing on Girder
ratio = 24.17 / 71.57
= 0.34
PASS
Single Bolt Shear Strength

Bolt shear stress
bolt grade
 = A325-N
Fnv
 = 54.0
[ksi]
AISC 14th  Table J3.2
bolt dia db
 = 0.750
[in]
bolt area Ab
 = 0.442
[in2]

Single bolt shear strength
Rn-bolt
 = Fnv Ab
 = 23.86
[kips]
AISC 14th  Eq J3-1
Bolt Bearing/TearOut Strength on Plate


Bolt hole diameter
bolt dia db
 = 3⁄4
[in]
bolt hole dia dh
 = 13⁄16
[in]
AISC 14th  Table J3.3
Bolt spacing
spacing Ls
 = 3.000
[in]

Plate tensile strength
Fu
 = 65.0
[ksi]

Plate thickness
t
 = 0.295
[in]

Interior Bolt


Bolt hole edge clear distance
Lc
 = Ls - dh
 = 2.188
[in]

Bolt tear out/bearing strength
Rn-t&b-in
 = 1.5 Lc t Fu ≤ 3.0 db t m Fu
AISC 14th  Eq J3-6b
 = 62.92 ≤ 43.14
 = 43.14
[kips]

Bolt strength at interior
Rn-in
 = min ( Rn-t&b-in , Rn-bolt )
 = 23.86
[kips]


Number of bolt
interior nin
 = 4

Bolt bearing strength for all bolts
Rn
 = nin Rn-in
 = 95.43
[kips]

Required shear strength
Vu
 = 
 = 24.17
[kips]

Bolt resistance factor-LRFD
φ
 = 0.75
AISC 14th  J3-10
φ Rn
 = 
 = 71.57
[kips]

ratio
 = 0.34
 > Vu
OK
 
 
Bolt Tensile Prying Action on End Plate
ratio = 0.13 / 8.55
= 0.01
PASS
Bolt group forces
shear V
 = 24.17
[kips]
axial P
 = -0.51
[kips]


Single Bolt Tensile Capacity Without Considering Prying
Bolt grade
grade
 = A325-N

Nominal tensile/shear stress
Fnt
 = 90.0
[ksi]
Fnv
 = 54.0
[ksi]
AISC 14th  Table J3.2
bolt dia db
 = 0.750
[in]
bolt area Ab
 = 0.442
[in2]

Bolt group shear force
shear V
 = 24.17
[kips]
no of bolt n
 = 4

Shear stress required
frv
 = V / ( n Ab )
 = 13.68
[ksi]

Resistance factor-LRFD
φ
 = 0.75
AISC 14th  J3.7
Modified nominal tensile stress
F'nt
 = 1.3 Fnt -
Fnt/φ Fnv
frv ≤ Fnt
 = 86.61
[ksi]
AISC 14th  Eq J3-3a
Bolt norminal tensile strength
rn
 = F'nt Ab
 = 38.26
[kips]
AISC 14th  Eq J3-1
Resistance factor-LRFD
φ
 = 0.75
AISC 14th  J3.6
Single bolt tensile capacity
φ rn
 = 
 = 28.70
[kips]


Single Bolt Tensile Capacity After Considering Prying
End plate
width w
 = 6.250
[in]
bolt gage g
 = 3.500
[in]

web tw
 = 0.375
[in]


Dist from bolt center to plate edge
a
 = 0.5 (w - g)
 = 1.375
[in]

a'
 = a + 0.5 db ≤ (1.25 b + 0.5 db )
 = 1.750
[in]
AISC 14th  Eq 9-27

Bolt hole diameter
bolt dia db
 = 0.750
[in]
bolt hole dia dh
 = 0.813
[in]
AISC 14th  B4.3b
Dist from bolt center to face of web
b
 = 0.5(g - tw )
 = 1.563
[in]

b'
 = b - 0.5 db
 = 1.188
[in]
AISC 14th  Eq 9-21

Bolt pitch spacing
sv
 = 3.000

Bolt tributary length
p
 = sv     p ≤ 2b  and p ≤ sv
 = 2.875
[in]
AISC 14th  Page 9-11

ρ
 = b' / a'
 = 0.679
AISC 14th  Eq 9-26
δ
 = 1 - dh / p
 = 0.717
AISC 14th  Eq 9-24
Tensile capacity per bolt before considering prying
B
 = from calc shown in above section
 = 28.70
[kips]

Resistance factor-LRFD
φ
 = 0.90
AISC 14th  Page 9-10
End plate thickness
t
 = 0.375
[in]
tensile Fu
 = 65.0
[ksi]

Plate thickness req'd to develop bolt tensile capacity without prying
tc
 = (
4 B b'/φ p Fu
)0.5
 = 0.900
[in]
AISC 14th  Eq 9-30a
α'
 = 
1/δ (1 + ρ )
[ (
tc/t
)2 - 1 ]
 = 3.955
AISC 14th  Eq 9-35
when  α' > 1
Q
 = (
t/tc
)2 (1 + δ )
 = 0.298
AISC 14th  Eq 9-34
 
Bolt tensile force per bolt in demand
T
 = from calc shown below
 = 0.13
[kips]

 
Tensile strength per bolt after considering prying
φ rn
 = B x Q
 = 8.55
[kips]
AISC 14th  Eq 9-31
ratio
 = 0.01
 > T
OK

Calculate Max Single Bolt Tensile Load
Bolt group force
axial P
 = 0.51
[kips]

 
Bolt number
Bolt Row nh
 = 2
Bolt Col nv
 = 2

Bolt tensile force per bolt
T
 = P / ( nv nh )
 = 0.13
[kips]

 
 
Gusset Plate to End Plate Weld Strength
ratio = 2.65 / 10.97
= 0.24
PASS
Weld Group Forces
shear V
 = 24.17
[kips]
axial P
 = -0.51
[kips]   in tension
 
Gusset-end plate fillet weld length
L
 = weld length tributary to bolt group
 = 9.108
[in]

 
Combined Weld Stress
Weld stress from axial force
fa
 = P / L
 = -0.056
[kip/in]
in tension
Weld stress from shear force
fv
 = V / L
 = 2.654
[kip/in]

Weld stress combined - max
fmax
 = ( f2a + f2v )0.5
 = 2.654
[kip/in]
AISC 14th  Eq 8-11
Weld stress load angle
θ
 = tan-1 (
fa/fv
)
 = 1.2
[°]

Fillet Weld Strength Calc
Fillet weld leg size
w
 = 5⁄16
[in]
load angle θ
 = 1.2
[°]

Electrode strength
FEXX
 = 70.0
[ksi]
strength coeff C1
 = 1.00
AISC 14th  Table 8-3
Number of weld line
n
 = 2   for double fillet

Load angle coefficient
C2
 = ( 1 + 0.5 sin1.5 θ )
 = 1.00
AISC 14th  Page 8-9
Fillet weld shear strength
Rn-w
 = 0.6 (C1 x 70 ksi) 0.707 w n C2
 = 18.587
[kip/in]
AISC 14th  Eq 8-1

Base metal - gusset plate
thickness t
 = 0.375
[in]
tensile Fu
 = 65.0
[ksi]

Base metal - gusset plate is in shear, shear rupture as per AISC 14th  Eq J4-4 is checked
AISC 14th  J2.4
Base metal shear rupture
Rn-b
 = 0.6 Fu t
 = 14.625
[kip/in]
AISC 14th  Eq J4-4

Double fillet linear shear strength
Rn
 = min ( Rn-w , Rn-b )
 = 14.625
[kip/in]
AISC 14th  Eq 9-2
Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq 8-1
φ Rn
 = 
 = 10.969
[kip/in]

ratio
 = 0.24
 > fmax
OK
 
 
 
Left Brace - Gusset to Beam
Direct Weld Connection
Code=AISC 360-10 LRFD
 
Result Summary
geometries & weld limitations = PASS
limit states max ratio 
= 0.21
PASS
 
 
Brace Weld Limitation Checks - Gusset to Beam
PASS
Min Fillet Weld Size

Thinner part joined thickness
t
 = 
 = 0.375
[in]

Min fillet weld size allowed
wmin
 = 
 = 0.188
[in]
AISC 14th  Table J2.4
Fillet weld size provided
w
 = 
 = 0.313
[in]

 > wmin
OK
Min Fillet Weld Length

Fillet weld size provided
w
 = 
 = 0.313
[in]

Min fillet weld length allowed
Lmin
 = 4 x w
 = 1.250
[in]
AISC 14th  J2.2b
Min fillet weld length
L
 = 
 = 13.298
[in]

 > Lmin
OK
 
 
 
 
Brace Force Load Case 1
Gusset plate t=0.375
P =35.00 kips (C)
ratio = 0.21
PASS
Gusset Plate - Shear Yielding
ratio = 24.24 / 149.60
= 0.16
PASS
Plate Shear Yielding Check


Plate size
width bp
 = 13.298
[in]
thickness tp
 = 0.375
[in]

Plate yield strength
Fy
 = 50.0
[ksi]

Plate gross area in shear
Agv
 = bp tp
 = 4.987
[in2]

Shear force required
Vu
 = 
 = 24.24
[kips]

Plate shear yielding strength
Rn
 = 0.6 Fy Agv
 = 149.60
[kips]
AISC 14th  Eq J4-3
Resistance factor-LRFD
φ
 = 1.00
AISC 14th  Eq J4-3
φ Rn
 = 
 = 149.60
[kips]

ratio
 = 0.16
 > Vu
OK
 
Gusset Plate - Shear Rupture
ratio = 24.24 / 145.86
= 0.17
PASS
Plate Shear Rupture Check


Plate size
width bp
 = 13.298
[in]
thickness tp
 = 0.375
[in]

Plate tensile strength
Fu
 = 65.0
[ksi]

Plate net area in shear
Anv
 = bp tp
 = 4.987
[in2]

Shear force in demand
Vu
 = 
 = 24.24
[kips]

Plate shear rupture strength
Rn
 = 0.6 Fu Anv
 = 194.48
[kips]
AISC 14th  Eq J4-4
Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq J4-4
φ Rn
 = 
 = 145.86
[kips]

ratio
 = 0.17
 > Vu
OK
 
 
Gusset Plate - Axial Tensile Yield
ratio = 0.58 / 224.40
= 0.00
PASS
Plate Tensile Yielding Check


Plate size
width bp
 = 13.298
[in]
thickness tp
 = 0.375
[in]

Plate yield strength
Fy
 = 50.0
[ksi]

Plate gross area in shear
Ag
 = bp tp
 = 4.987
[in2]

Tensile force required
Pu
 = 
 = 0.58
[kips]

Plate tensile yielding strength
Rn
 = Fy Ag
 = 249.34
[kips]
AISC 14th  Eq J4-1
Resistance factor-LRFD
φ
 = 0.90
AISC 14th  Eq J4-1
φ Rn
 = 
 = 224.40
[kips]

ratio
 = 0.00
 > Pu
OK
 
 
Gusset Plate - Flexural Yield Interact
ratio =
= 0.03
PASS
Gusset plate
width bp
 = 13.298
[in]
thick tp
 = 0.375
[in]

yield Fy
 = 50.0
[ksi]

Shear plate - gross area
Ag
 = bp x tp
 = 4.987
[in2]

Shear plate - plastic modulus
Zp
 = ( bp x t2p ) / 4
 = 16.578
[in3]

Flexural strength available
Mc
 = φ Fy Zp     φ=0.90
 = 62.17
[kip-ft]

Flexural strength required
Mr
 = from gusset interface forces calc
 = 0.00
[kip-ft]

 
Axial strength available
Pc
 = from axial tensile yield check
 = 224.40
[kips]

Axial strength required
Pr
 = from gusset interface forces calc
 = 0.58
[kips]

 
Shear strength available
Vc
 = from shear yielding check
 = 149.60
[kips]

Shear strength required
Vr
 = from gusset interface forces calc
 = 24.24
[kips]

 
Flexural yield interaction
ratio
 = (
Vr/Vc
)2 + (
Pr/Pc
+
Mr/Mc
)2
 = 0.03
AISC 14th  Eq 10-5
 < 1.0
OK
 
Gusset Plate - Flexural Rupture Interact
ratio =
= 0.03
PASS
Gusset plate
width bp
 = 13.298
[in]
thick tp
 = 0.375
[in]

tensile Fu
 = 65.0
[ksi]

Net area of plate
An
 = bp x tp
 = 4.987
[in2]

Plastic modulus of net section
Znet
 = ( bp x t2p ) / 4
 = 16.578
[in3]

Flexural strength available
Mc
 = φ Fu Znet     φ=0.75
 = 67.35
[kip-ft]

Flexural strength required
Mr
 = from gusset interface forces calc
 = 0.00
[kip-ft]

 
Shear strength available
Vc
 = from shear rupture check
 = 145.86
[kips]

Shear strength required
Vr
 = from gusset interface forces calc
 = 24.24
[kips]

 
Flexural rupture interaction
ratio
 = (
Vr/Vc
)2 + (
Mr/Mc
)2
 = 0.03
AISC 14th  Eq 10-5
 < 1.0
OK
 
 
Gusset to Beam Weld Strength
ratio = 1.82 / 8.78
= 0.21
PASS
Gusset to Beam Interface - Forces
shear Hb
 = 24.24
[kips]
axial Vb
 = 0.58
[kips]   in compression
moment Mb
 = 0.00
[kip-ft]

 
Gusset-beam fillet weld length
Lw
 = 
 = 13.298
[in]

Gusset to Beam Interface - Combined Weld Stress
Weld stress from axial force
fa
 = Vb / Lwb
 = 0.000
[kip/in]
in compression
Weld stress from shear force
fv
 = Hb / Lwb
 = 1.823
[kip/in]

Weld stress from moment force
fb
 = 
M/L2 / 6
 = 0.000
[kip/in]

Weld stress combined - max
fmax
 = fv
 = 1.823
[kip/in]
AISC 14th  Eq 8-11
Weld resultant load angle
θ
 = weld only has shear component
 = 0.0
[°]

Fillet Weld Strength Calc
Fillet weld leg size
w
 = 5⁄16
[in]
load angle θ
 = 0.0
[°]

Electrode strength
FEXX
 = 70.0
[ksi]
strength coeff C1
 = 1.00
AISC 14th  Table 8-3
Number of weld line
n
 = 2   for double fillet

Load angle coefficient
C2
 = ( 1 + 0.5 sin1.5 θ )
 = 1.00
AISC 14th  Page 8-9
Fillet weld shear strength
Rn-w
 = 0.6 (C1 x 70 ksi) 0.707 w n C2
 = 18.559
[kip/in]
AISC 14th  Eq 8-1

Base metal - gusset plate
thickness t
 = 0.375
[in]
tensile Fu
 = 65.0
[ksi]

Base metal - gusset plate is in shear, shear rupture as per AISC 14th  Eq J4-4 is checked
AISC 14th  J2.4
Base metal shear rupture
Rn-b
 = 0.6 Fu t
 = 14.625
[kip/in]
AISC 14th  Eq J4-4

Double fillet linear shear strength
Rn
 = min ( Rn-w , Rn-b )
 = 14.625
[kip/in]
AISC 14th  Eq 9-2
Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq 8-1
φ Rn
 = 
 = 10.969
[kip/in]

 
When gusset plate is directly welded to beam or column, apply 1.25 ductility factor
to allow adequate force redistribution in the weld group
AISC 14th  Page 13-11
 
Weld strength used for design after applying ductility factor
φ Rn
 = φ Rn x ( 1/1.25 )
 = 8.775
[kip/in]

ratio
 = 0.21
 > fmax
OK
 
 
 
 
Brace Force Load Case 2
Gusset plate t=0.375
P =-35.00 kips (T)
ratio = 0.21
PASS
Gusset Plate - Shear Yielding
ratio = 24.24 / 149.60
= 0.16
PASS
Plate Shear Yielding Check


Plate size
width bp
 = 13.298
[in]
thickness tp
 = 0.375
[in]

Plate yield strength
Fy
 = 50.0
[ksi]

Plate gross area in shear
Agv
 = bp tp
 = 4.987
[in2]

Shear force required
Vu
 = 
 = 24.24
[kips]

Plate shear yielding strength
Rn
 = 0.6 Fy Agv
 = 149.60
[kips]
AISC 14th  Eq J4-3
Resistance factor-LRFD
φ
 = 1.00
AISC 14th  Eq J4-3
φ Rn
 = 
 = 149.60
[kips]

ratio
 = 0.16
 > Vu
OK
 
Gusset Plate - Shear Rupture
ratio = 24.24 / 145.86
= 0.17
PASS
Plate Shear Rupture Check


Plate size
width bp
 = 13.298
[in]
thickness tp
 = 0.375
[in]

Plate tensile strength
Fu
 = 65.0
[ksi]

Plate net area in shear
Anv
 = bp tp
 = 4.987
[in2]

Shear force in demand
Vu
 = 
 = 24.24
[kips]

Plate shear rupture strength
Rn
 = 0.6 Fu Anv
 = 194.48
[kips]
AISC 14th  Eq J4-4
Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq J4-4
φ Rn
 = 
 = 145.86
[kips]

ratio
 = 0.17
 > Vu
OK
 
 
Gusset Plate - Axial Yield
ratio = 0.58 / 224.40
= 0.00
PASS
Plate Tensile Yielding Check


Plate size
width bp
 = 13.298
[in]
thickness tp
 = 0.375
[in]

Plate yield strength
Fy
 = 50.0
[ksi]

Plate gross area in shear
Ag
 = bp tp
 = 4.987
[in2]

Tensile force required
Pu
 = 
 = 0.58
[kips]

Plate tensile yielding strength
Rn
 = Fy Ag
 = 249.34
[kips]
AISC 14th  Eq J4-1
Resistance factor-LRFD
φ
 = 0.90
AISC 14th  Eq J4-1
φ Rn
 = 
 = 224.40
[kips]

ratio
 = 0.00
 > Pu
OK
 
Gusset Plate - Axial Tensile Rupture
ratio = 0.58 / 243.10
= 0.00
PASS
Plate Tensile Rupture Check


Plate size
width bp
 = 13.298
[in]
thickness tp
 = 0.375
[in]

Plate tensile strength
Fu
 = 65.0
[ksi]

Plate net area in tension
Ant
 = bp tp
 = 4.987
[in2]

Tensile force required
Pu
 = 
 = 0.58
[kips]

Plate tensile rupture strength
Rn
 = Fu Ant
 = 324.14
[kips]
AISC 14th  Eq J4-2
Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq J4-2
φ Rn
 = 
 = 243.10
[kips]
AISC 14th  Eq J4-2
ratio
 = 0.00
 > Pu
OK
 
 
Gusset Plate - Flexural Yield Interact
ratio =
= 0.03
PASS
Gusset plate
width bp
 = 13.298
[in]
thick tp
 = 0.375
[in]

yield Fy
 = 50.0
[ksi]

Shear plate - gross area
Ag
 = bp x tp
 = 4.987
[in2]

Shear plate - plastic modulus
Zp
 = ( bp x t2p ) / 4
 = 16.578
[in3]

Flexural strength available
Mc
 = φ Fy Zp     φ=0.90
 = 62.17
[kip-ft]

Flexural strength required
Mr
 = from gusset interface forces calc
 = 0.00
[kip-ft]

 
Axial strength available
Pc
 = from axial tensile yield check
 = 224.40
[kips]

Axial strength required
Pr
 = from gusset interface forces calc
 = 0.58
[kips]

 
Shear strength available
Vc
 = from shear yielding check
 = 149.60
[kips]

Shear strength required
Vr
 = from gusset interface forces calc
 = 24.24
[kips]

 
Flexural yield interaction
ratio
 = (
Vr/Vc
)2 + (
Pr/Pc
+
Mr/Mc
)2
 = 0.03
AISC 14th  Eq 10-5
 < 1.0
OK
 
Gusset Plate - Flexural Rupture Interact
ratio =
= 0.03
PASS
Gusset plate
width bp
 = 13.298
[in]
thick tp
 = 0.375
[in]

tensile Fu
 = 65.0
[ksi]

Net area of plate
An
 = bp x tp
 = 4.987
[in2]

Plastic modulus of net section
Znet
 = ( bp x t2p ) / 4
 = 16.578
[in3]

Flexural strength available
Mc
 = φ Fu Znet     φ=0.75
 = 67.35
[kip-ft]

Flexural strength required
Mr
 = from gusset interface forces calc
 = 0.00
[kip-ft]

 
Axial strength available
Pc
 = from axial tensile rupture check
 = 243.10
[kips]

Axial strength required
Pr
 = from gusset interface forces calc
 = 0.58
[kips]

 
Shear strength available
Vc
 = from shear rupture check
 = 145.86
[kips]

Shear strength required
Vr
 = from gusset interface forces calc
 = 24.24
[kips]

 
Flexural rupture interaction
ratio
 = (
Vr/Vc
)2 + (
Pr/Pc
+
Mr/Mc
)2
 = 0.03
AISC 14th  Eq 10-5
 < 1.0
OK
 
 
Gusset to Beam Weld Strength
ratio = 1.82 / 8.78
= 0.21
PASS
Gusset to Beam Interface - Forces
shear Hb
 = 24.24
[kips]
axial Vb
 = -0.58
[kips]   in tension
moment Mb
 = 0.00
[kip-ft]

 
Gusset-beam fillet weld length
Lw
 = 
 = 13.298
[in]

Gusset to Beam Interface - Combined Weld Stress
Weld stress from axial force
fa
 = Vb / Lwb
 = -0.044
[kip/in]
in tension
Weld stress from shear force
fv
 = Hb / Lwb
 = 1.823
[kip/in]

Weld stress from moment force
fb
 = 
M/L2 / 6
 = 0.000
[kip/in]

Weld stress combined - max
fmax
 = [ (fa - fb )2 + f2v ]0.5
 = 1.823
[kip/in]
AISC 14th  Eq 8-11
Weld resultant load angle
θ
 = tan-1 [( fb - fa ) / fv ]
 = 1.4
[°]

Fillet Weld Strength Calc
Fillet weld leg size
w
 = 5⁄16
[in]
load angle θ
 = 1.4
[°]

Electrode strength
FEXX
 = 70.0
[ksi]
strength coeff C1
 = 1.00
AISC 14th  Table 8-3
Number of weld line
n
 = 2   for double fillet

Load angle coefficient
C2
 = ( 1 + 0.5 sin1.5 θ )
 = 1.00
AISC 14th  Page 8-9
Fillet weld shear strength
Rn-w
 = 0.6 (C1 x 70 ksi) 0.707 w n C2
 = 18.593
[kip/in]
AISC 14th  Eq 8-1

Base metal - gusset plate
thickness t
 = 0.375
[in]
tensile Fu
 = 65.0
[ksi]

Base metal - gusset plate is in shear, shear rupture as per AISC 14th  Eq J4-4 is checked
AISC 14th  J2.4
Base metal shear rupture
Rn-b
 = 0.6 Fu t
 = 14.625
[kip/in]
AISC 14th  Eq J4-4

Double fillet linear shear strength
Rn
 = min ( Rn-w , Rn-b )
 = 14.625
[kip/in]
AISC 14th  Eq 9-2
Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq 8-1
φ Rn
 = 
 = 10.969
[kip/in]

 
When gusset plate is directly welded to beam or column, apply 1.25 ductility factor
to allow adequate force redistribution in the weld group
AISC 14th  Page 13-11
 
Weld strength used for design after applying ductility factor
φ Rn
 = φ Rn x ( 1/1.25 )
 = 8.775
[kip/in]

ratio
 = 0.21
 > fmax
OK
 
 
Beam Web Local Yielding
ratio = 0.58 / 267.97
= 0.00
PASS
 
Concentrated force from gusset
Pu
 = 
 = 0.58
[kips]

Beam section
d
 = 12.100
[in]
tf
 = 0.575
[in]

tw
 = 0.335
[in]
k
 = 1.080
[in]

yield Fy
 = 50.0
[ksi]


Length of bearing
lb
 = Gusset/Beam interface length
 = 13.298
[in]

Gusset plate corner clip
clip
 = from user input
 = 0.750
[in]

Distance from normal force applied point to member end
lN
 = 0.5 lb + clip
 = 7.399
[in]

 
when lN  ≤ d , use AISC 14th  Eq J10-3
AISC 14th  Eq J10-3
 
Beam web local yielding strength
Rn
 = Fy tw ( 2.5 k + lb )
 = 267.97
[kips]
AISC 14th  Eq J10-3
Resistance factor-LRFD
φ
 = 1.00
φ Rn
 = 
 = 267.97
[kips]

ratio
 = 0.00
 > Pu
OK
 
 
Beam to Column
End Plate Connection
Code=AISC 360-10 LRFD
 
Result Summary
geometries & weld limitations = PASS
limit states max ratio 
= 0.47
PASS
 
Geometry Restriction Check - End Plate to Column Web
PASS
Min Bolt Edge Distance - End Plate to Column Web

Bolt diameter
db
 = 
 = 0.750
[in]

Min edge distance allowed
Le-min
 = 
 = 1.000
[in]
AISC 14th  Table J3.4
Min edge distance in End Plate to Column Web
Le
 = 
 = 1.375
[in]

 > Le-min
OK
Min Bolt Spacing - End Plate to Column Web

Bolt diameter
db
 = 
 = 0.750
[in]

Min bolt spacing allowed
Ls-min
 = 2.667 db
 = 2.000
[in]
AISC 14th  J3.3
Min Bolt spacing in End Plate to Column Web
Ls
 = 
 = 3.500
[in]

 > Ls-min
OK
 
Weld Limitation Check - Beam Web to End Plate
PASS
Min Fillet Weld Size

Thinner part joined thickness
t
 = 
 = 0.335
[in]

Min fillet weld size allowed
wmin
 = 
 = 0.188
[in]
AISC 14th  Table J2.4
Fillet weld size provided
w
 = 
 = 0.375
[in]

 > wmin
OK
Min Fillet Weld Length

Fillet weld size provided
w
 = 
 = 0.375
[in]

Min fillet weld length allowed
Lmin
 = 4 x w
 = 1.500
[in]
AISC 14th  J2.2b
Min fillet weld length
L
 = 
 = 9.350
[in]

 > Lmin
OK
 
 
 
 
Brace Force Load Case 1
shear V = 23.84 kips     axial P = -15.00 kips (T)
ratio = 0.47
PASS
Beam - Shear Yielding - Vy
ratio = 25.00 / 121.61
= 0.21
PASS
Section Shear Yielding Check


Sect yield strength
Fy
 = 50.0
[ksi]

Sect gross area in shear
Agv
 = 
 = 4.054
[in2]

Shear force required
Vu
 = 
 = 25.00
[kips]

Sect shear yielding strength
Rn
 = 0.6 Fy Agv
 = 121.61
[kips]
AISC 14th  Eq J4-3
Resistance factor-LRFD
φ
 = 1.00
AISC 14th  Eq J4-3
φ Rn
 = 
 = 121.61
[kips]

ratio
 = 0.21
 > Vu
OK
 
Beam - Shear Rupture - Vy
ratio = 25.00 / 118.56
= 0.21
PASS
Section Shear Rupture Check


Sect tensile strength
Fu
 = 65.0
[ksi]

Sect net area in shear
Anv
 = 
 = 4.054
[in2]

Shear force in demand
Vu
 = 
 = 25.00
[kips]

Sect shear rupture strength
Rn
 = 0.6 Fu Anv
 = 158.09
[kips]
AISC 14th  Eq J4-4
Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq J4-4
φ Rn
 = 
 = 118.56
[kips]

ratio
 = 0.21
 > Vu
OK
 
Beam - Shear Yielding - Vz
ratio = 23.84 / 277.73
= 0.09
PASS
Section Shear Yielding Check


Sect yield strength
Fy
 = 50.0
[ksi]

Sect gross area in shear
Agv
 = 
 = 9.258
[in2]

Shear force required
Vu
 = 
 = 23.84
[kips]

Sect shear yielding strength
Rn
 = 0.6 Fy Agv
 = 277.73
[kips]
AISC 14th  Eq J4-3
Resistance factor-LRFD
φ
 = 1.00
AISC 14th  Eq J4-3
φ Rn
 = 
 = 277.73
[kips]

ratio
 = 0.09
 > Vu
OK
 
Beam - Shear Rupture - Vz
ratio = 23.84 / 270.78
= 0.09
PASS
Section Shear Rupture Check


Sect tensile strength
Fu
 = 65.0
[ksi]

Sect net area in shear
Anv
 = 
 = 9.258
[in2]

Shear force in demand
Vu
 = 
 = 23.84
[kips]

Sect shear rupture strength
Rn
 = 0.6 Fu Anv
 = 361.04
[kips]
AISC 14th  Eq J4-4
Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq J4-4
φ Rn
 = 
 = 270.78
[kips]

ratio
 = 0.09
 > Vu
OK
 
Beam - Axial Tensile Yield - Px
ratio = 15.00 / 589.50
= 0.03
PASS
Gross area subject to tension
Ag
 = 
 = 13.100
[in2]

Steel yield strength
Fy
 = 
 = 50.0
[ksi]

Tensile force required
Pu
 = 
 = 15.00
[kips]

Tensile yielding strength
Rn
 = Fy Ag
 = 655.00
[kips]
AISC 14th  Eq D2-1
Resistance factor-LRFD
φ
 = 0.90
AISC 14th  D2 (a)
φ Rn
 = 
 = 589.50
[kips]
AISC 14th  Eq D2-1
ratio
 = 0.03
 > Pu
OK
 
Beam Web - Axial Tensile Rupture - Px
ratio = 15.00 / 140.45
= 0.11
PASS
End Plate Direct Connect Length Calc
Beam web-end plate weld length
L
 = 
 = 9.350
[in]

Beam web-end plate fillet weld size
w
 = 
 = 0.375
[in]

Beam web-end plate connect length
Lw
 = L - 2 w
 = 8.600
[in]

Plate Tensile Rupture Check


Plate size
width bp
 = 8.600
[in]
thickness tp
 = 0.335
[in]

Plate tensile strength
Fu
 = 65.0
[ksi]

Plate net area in tension
Ant
 = bp tp
 = 2.881
[in2]

Tensile force in demand
Pu
 = 
 = 15.00
[kips]

Plate tensile rupture strength
Rn
 = Fu Ant
 = 187.27
[kips]
AISC 14th  Eq J4-2
Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq J4-2
φ Rn
 = 
 = 140.45
[kips]
AISC 14th  Eq J4-2
ratio
 = 0.11
 > Pu
OK
 
 
End Plate - Shear Yielding - Vy
ratio = 12.50 / 109.69
= 0.11
PASS
Plate Shear Yielding Check


Plate size
width bp
 = 9.750
[in]
thickness tp
 = 0.375
[in]

Plate yield strength
Fy
 = 50.0
[ksi]

Plate gross area in shear
Agv
 = bp tp
 = 3.656
[in2]

Shear force required
Vu
 = 
 = 12.50
[kips]

Plate shear yielding strength
Rn
 = 0.6 Fy Agv
 = 109.69
[kips]
AISC 14th  Eq J4-3
Resistance factor-LRFD
φ
 = 1.00
AISC 14th  Eq J4-3
φ Rn
 = 
 = 109.69
[kips]

ratio
 = 0.11
 > Vu
OK
 
End Plate - Shear Rupture - Vy
ratio = 12.50 / 78.15
= 0.16
PASS
Plate Shear Rupture Check


Bolt hole diameter
bolt dia db
 = 3⁄4
[in]
bolt hole dia dh
 = 7⁄8
[in]
AISC 14th  B4.3b
Number of bolt
n
 = 3

Plate size
width bp
 = 9.750
[in]
thickness tp
 = 0.375
[in]

Plate tensile strength
Fu
 = 65.0
[ksi]

Plate net area in shear
Anv
 = ( bp - n dh ) tp
 = 2.672
[in2]

Shear force required
Vu
 = 
 = 12.50
[kips]

Plate shear rupture strength
Rn
 = 0.6 Fu Anv
 = 104.20
[kips]
AISC 14th  Eq J4-4
Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq J4-4
φ Rn
 = 
 = 78.15
[kips]

ratio
 = 0.16
 > Vu
OK
 
End Plate - Shear Yielding - Vz
ratio = 11.92 / 75.94
= 0.16
PASS
Plate Shear Yielding Check


Plate size
width bp
 = 6.750
[in]
thickness tp
 = 0.375
[in]

Plate yield strength
Fy
 = 50.0
[ksi]

Plate gross area in shear
Agv
 = bp tp
 = 2.531
[in2]

Shear force required
Vu
 = 
 = 11.92
[kips]

Plate shear yielding strength
Rn
 = 0.6 Fy Agv
 = 75.94
[kips]
AISC 14th  Eq J4-3
Resistance factor-LRFD
φ
 = 1.00
AISC 14th  Eq J4-3
φ Rn
 = 
 = 75.94
[kips]

ratio
 = 0.16
 > Vu
OK
 
End Plate - Shear Rupture - Vz
ratio = 11.92 / 54.84
= 0.22
PASS
Plate Shear Rupture Check


Bolt hole diameter
bolt dia db
 = 3⁄4
[in]
bolt hole dia dh
 = 7⁄8
[in]
AISC 14th  B4.3b
Number of bolt
n
 = 2

Plate size
width bp
 = 6.750
[in]
thickness tp
 = 0.375
[in]

Plate tensile strength
Fu
 = 65.0
[ksi]

Plate net area in shear
Anv
 = ( bp - n dh ) tp
 = 1.875
[in2]

Shear force required
Vu
 = 
 = 11.92
[kips]

Plate shear rupture strength
Rn
 = 0.6 Fu Anv
 = 73.13
[kips]
AISC 14th  Eq J4-4
Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq J4-4
φ Rn
 = 
 = 54.84
[kips]

ratio
 = 0.22
 > Vu
OK
 
 
Coped Beam - Flexural Rupture
ratio = 25.00 / 57.56
= 0.43
PASS
Beam section & cope side
sect
 = W12X45
cope side
 = double cope
Beam top flange cope
depth dc
 = 1.250
[in]
length Lc
 = 3.983
[in]

Beam bottom flange cope
depth dc
 = 1.250
[in]
length Lc
 = 3.983
[in]


Beam section elastic modulus
Snet
 = 
 = 5.146
[in3]

Beam section tensile strength
Fu
 = 
 = 65.0
[ksi]

Distance from face of cope to the point of inflection of beam
e
 = 
 = 4.358
[in]
AISC 14th  Page 9-6

Beam end shear force
Vu
 = 
 = 25.00
[kips]

Beam end shear resistance
Rn
 = Fu Snet / e
 = 76.75
[kips]
AISC 14th  Eq 9-4
Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq 9-4
φ Rn
 = 
 = 57.56
[kips]

ratio
 = 0.43
 > Vu
OK
 
Coped Beam - Local Web Buckling
ratio = 25.00 / 53.13
= 0.47
PASS
Beam section & cope side
sect
 = W12X45
cope side
 = double cope
Beam top flange cope
depth dct
 = 1.250
[in]
length Lct
 = 3.983
[in]

Beam bottom flange cope
depth dcb
 = 1.250
[in]
length Lcb
 = 3.983
[in]


Beam section elastic modulus
Snet
 = 
 = 5.146
[in3]

Distance from face of cope to the point of inflection of beam
e
 = 
 = 4.358
[in]
AISC 14th  Page 9-6

Beam section
depth d
 = 12.100
[in]
web tw
 = 0.335
[in]

Fy
 = 50.0
[ksi]
E
 = 29000
[ksi]

fd
 = 3.5 - 7.5 (dct / d)
 = 2.725
AISC 14th  Eq 9-13
Reduced beam depth
h0
 = d - dct - dcb
 = 9.600
[in]

Plate local buckling stress
Fcr
 = 0.62 π E
t2w/Lct h0
fd
 = 451.8
[ksi]
AISC 14th  Eq 9-12
Fcr
 = Fcr   ≤  Fy
 = 50.0
[ksi]
AISC 14th  Eq 9-12

Beam end shear force
Vu
 = 
 = 25.00
[kips]

Beam end shear resistance
Rn
 = Fcr Snet / e
 = 59.04
[kips]
AISC 14th  Eq 9-6
Resistance factor-LRFD
φ
 = 0.90
AISC 14th  Eq 9-6
φ Rn
 = 
 = 53.13
[kips]

ratio
 = 0.47
 > Vu
OK
 
 
End Plate - Bolt Bearing on End Plate - Vy Vz Combined
ratio = 34.54 / 107.35
= 0.32
PASS
The bolt group is oriented so that the shear Vy is in ver. direction and the shear Vz is in hor. direction
 
Bolt group forces
shear Vy
 = 25.00
[kips]
shear Vz
 = 23.84
[kips]

Bolt group resultant force
R
 = ( V2y + V2z )0.5
 = 34.54
[kips]

Resultant force/hor line load angle
θ
 = tan-1 (Vy / Vz )
 = 46.36
[°]


Bolt hole diameter
bolt dia db
 = 0.750
[in]
bolt hole dia dbh
 = 0.813
[in]
AISC 14th  B4.3b
Bolt hole ver. dimension
dv
 = 
 = 0.813
[in]

Bolt hole hor. dimension
dh
 = 
 = 0.813
[in]

Bolt center to bolt hole edge dist
dc
 = 0.5 dbh
 = 0.406
[in]


Bolt no in ver & hor direction
Bolt Row nv
 = 3
Bolt Col nh
 = 2

Bolt spacing
ver sv
 = 3.500
[in]
hor sh
 = 4.000
[in]

Bolt edge distance
ver ev
 = 1.375
[in]
hor eh
 = 1.375
[in]


Bolt clear dist - bot right corner bolt
LcA
 = min (
ev/sin θ
,
eh/cos θ
) - dc
 = 1.494
[in]

Bolt clear dist - right side edge bolt
LcB
 = min (
sv - 0.5dv/sin θ
,
eh/cos θ
) - dc
 = 1.586
[in]

Bolt clear dist - bot side edge bolt
LcC
 = min (
ev/sin θ
,
sh - 0.5dv/cos θ
) - dc
 = 1.494
[in]

Bolt clear dist - inner edge bolt
LcD
 = min (
sv - 0.5dv/sin θ
,
sh - 0.5dv/cos θ
) - dc
 = 3.869
[in]

Single Bolt Shear Strength

Bolt shear stress
bolt grade
 = A325-N
Fnv
 = 54.0
[ksi]
AISC 14th  Table J3.2
bolt dia db
 = 0.750
[in]
bolt area Ab
 = 0.442
[in2]

Single bolt shear strength
Rn-bolt
 = Fnv Ab
 = 23.86
[kips]
AISC 14th  Eq J3-1

Bolt bearing on plate
thick t
 = 0.375
[in]
tensile Fu
 = 65.0
[ksi]

Bolt bearing strength
Rn-br
 = 3.0 db t Fu
 = 54.84
[kips]
AISC 14th  Eq J3-6b

Type A - Bolt Group Bottom Right Corner Bolt
Number of bolt
nA
 = 1

Bolt tear out strength
Rn-tA
 = 1.5 LcA t Fu
 = 54.61
[kips]
AISC 14th  Eq J3-6b
Bolt bearing strength
RnA
 = min ( Rn-tA , Rn-br , Rn-bolt )
 = 23.86
[kips]


Type B - Bolt Group Right Side Edge Bolt
Number of bolt
nB
 = 2

Bolt tear out strength
Rn-tB
 = 1.5 LcB t Fu
 = 57.99
[kips]
AISC 14th  Eq J3-6b
Bolt bearing strength
RnB
 = min ( Rn-tB , Rn-br , Rn-bolt )
 = 23.86
[kips]


Type C - Bolt Group Bottom Side Edge Bolt
Number of bolt
nC
 = 1

Bolt tear out strength
Rn-tC
 = 1.5 LcC t Fu
 = 54.61
[kips]
AISC 14th  Eq J3-6b
Bolt bearing strength
RnC
 = min ( Rn-tC , Rn-br , Rn-bolt )
 = 23.86
[kips]


Type D - Bolt Group Inner Edge Bolt
Number of bolt
nD
 = 2

Bolt tear out strength
Rn-tD
 = 1.5 LcD t Fu
 = 141.45
[kips]
AISC 14th  Eq J3-6b
Bolt bearing strength
RnD
 = min ( Rn-tD , Rn-br , Rn-bolt )
 = 23.86
[kips]


Bolt bearing strength for all bolts
Rn
 = nA RnA + nB RnB + nC RnC + nD RnD
 = 143.14
[kips]

Bolt resistance factor-LRFD
φ
 = 0.75
AISC 14th  J3-10
φ Rn
 = 
 = 107.35
[kips]

ratio
 = 0.32
 > R
OK
 
End Plate - Bolt Bearing on Column Web - Vy Vz Combined
ratio = 34.54 / 107.35
= 0.32
PASS
The bolt group is oriented so that the shear Vy is in ver. direction and the shear Vz is in hor. direction
 
Bolt group forces
shear Vy
 = 25.00
[kips]
shear Vz
 = 23.84
[kips]

Bolt group resultant force
R
 = ( V2y + V2z )0.5
 = 34.54
[kips]

Resultant force/hor line load angle
θ
 = tan-1 (Vy / Vz )
 = 46.36
[°]


Bolt hole diameter
bolt dia db
 = 0.750
[in]
bolt hole dia dbh
 = 0.813
[in]
AISC 14th  B4.3b
Bolt hole ver. dimension
dv
 = 
 = 0.813
[in]

Bolt hole hor. dimension
dh
 = 
 = 0.813
[in]

Bolt center to bolt hole edge dist
dc
 = 0.5 dbh
 = 0.406
[in]


Bolt no in ver & hor direction
Bolt Row nv
 = 3
Bolt Col nh
 = 2

Bolt spacing
ver sv
 = 3.500
[in]
hor sh
 = 4.000
[in]

Bolt edge distance
ver ev
 = 1.375
[in]
hor eh
 = 1.375
[in]


Bolt clear dist - bot right corner bolt
LcA
 = min (
ev/sin θ
,
eh/cos θ
) - dc
 = 1.494
[in]

Bolt clear dist - right side edge bolt
LcB
 = min (
sv - 0.5dv/sin θ
,
eh/cos θ
) - dc
 = 1.586
[in]

Bolt clear dist - bot side edge bolt
LcC
 = min (
ev/sin θ
,
sh - 0.5dv/cos θ
) - dc
 = 1.494
[in]

Bolt clear dist - inner edge bolt
LcD
 = min (
sv - 0.5dv/sin θ
,
sh - 0.5dv/cos θ
) - dc
 = 3.869
[in]

Single Bolt Shear Strength

Bolt shear stress
bolt grade
 = A325-N
Fnv
 = 54.0
[ksi]
AISC 14th  Table J3.2
bolt dia db
 = 0.750
[in]
bolt area Ab
 = 0.442
[in2]

Single bolt shear strength
Rn-bolt
 = Fnv Ab
 = 23.86
[kips]
AISC 14th  Eq J3-1

Bolt bearing on plate
thick t
 = 0.295
[in]
tensile Fu
 = 65.0
[ksi]

Bolt bearing strength
Rn-br
 = 3.0 db t Fu
 = 43.14
[kips]
AISC 14th  Eq J3-6b

Type A - Bolt Group Bottom Right Corner Bolt
Number of bolt
nA
 = 1

Bolt tear out strength
Rn-tA
 = 1.5 LcA t Fu
 = 42.96
[kips]
AISC 14th  Eq J3-6b
Bolt bearing strength
RnA
 = min ( Rn-tA , Rn-br , Rn-bolt )
 = 23.86
[kips]


Type B - Bolt Group Right Side Edge Bolt
Number of bolt
nB
 = 2

Bolt tear out strength
Rn-tB
 = 1.5 LcB t Fu
 = 45.62
[kips]
AISC 14th  Eq J3-6b
Bolt bearing strength
RnB
 = min ( Rn-tB , Rn-br , Rn-bolt )
 = 23.86
[kips]


Type C - Bolt Group Bottom Side Edge Bolt
Number of bolt
nC
 = 1

Bolt tear out strength
Rn-tC
 = 1.5 LcC t Fu
 = 42.96
[kips]
AISC 14th  Eq J3-6b
Bolt bearing strength
RnC
 = min ( Rn-tC , Rn-br , Rn-bolt )
 = 23.86
[kips]


Type D - Bolt Group Inner Edge Bolt
Number of bolt
nD
 = 2

Bolt tear out strength
Rn-tD
 = 1.5 LcD t Fu
 = 111.27
[kips]
AISC 14th  Eq J3-6b
Bolt bearing strength
RnD
 = min ( Rn-tD , Rn-br , Rn-bolt )
 = 23.86
[kips]


Bolt bearing strength for all bolts
Rn
 = nA RnA + nB RnB + nC RnC + nD RnD
 = 143.14
[kips]

Bolt resistance factor-LRFD
φ
 = 0.75
AISC 14th  J3-10
φ Rn
 = 
 = 107.35
[kips]

ratio
 = 0.32
 > R
OK
 
 
End Plate - Shear in Vy - Block Shear - Center Strip
ratio = 25.00 / 192.87
= 0.13
PASS
Plate Block Shear - Center Strip


Bolt hole diameter
bolt dia db
 = 3⁄4
[in]
bolt hole dia dh
 = 7⁄8
[in]
AISC 14th  B4.3b
Plate thickness
tp
 = 0.375
[in]

Plate strength
Fy
 = 50.0
[ksi]
Fu
 = 65.0
[ksi]

Bolt no in ver & hor dir
nv
 = 2
nh
 = 3

Bolt spacing in ver & hor dir
sv
 = 4.000
[in]
sh
 = 3.500
[in]

Bolt edge dist in ver & hor dir
ev
 = 1.375
[in]
eh
 = 1.375
[in]


Gross area subject to shear
Agv
 = [ (nh - 1) sh + eh ] tp x 2
 = 6.281
[in2]

Net area subject to shear
Anv
 = Agv - [(nh - 1)+ 0.5] dh tp x2
 = 4.641
[in2]

Net area subject to tension
when sheared out by center strip
Ant
 = ( nv - 1) ( sv - dh ) tp
 = 1.172
[in2]


Block shear strength required
Vu
 = 
 = 25.00
[kips]

Uniform tension stress factor
Ubs
 = 1.00
AISC 14th  Fig C-J4.2
Bolt shear resistance provided
Rn
 = min (0.6Fu Anv , 0.6Fy Agv ) +
 = 257.16
[kips]
AISC 14th  Eq J4-5
Ubs Fu Ant

Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq J4-5
φ Rn
 = 
 = 192.87
[kips]

ratio
 = 0.13
 > Vu
OK
 
End Plate - Shear in Vy - Block Shear - 2-Side Strip
ratio = 25.00 / 170.02
= 0.15
PASS
Plate Block Shear - 2 Side Strips


Bolt hole diameter
bolt dia db
 = 3⁄4
[in]
bolt hole dia dh
 = 7⁄8
[in]
AISC 14th  B4.3b
Plate thickness
tp
 = 0.375
[in]

Plate strength
Fy
 = 50.0
[ksi]
Fu
 = 65.0
[ksi]

Bolt no in ver & hor dir
nv
 = 2
nh
 = 3

Bolt spacing in ver & hor dir
sv
 = 4.000
[in]
sh
 = 3.500
[in]

Bolt edge dist in ver & hor dir
ev
 = 1.375
[in]
eh
 = 1.375
[in]


Gross area subject to shear
Agv
 = [ (nh - 1) sh + eh ] tp x 2
 = 6.281
[in2]

Net area subject to shear
Anv
 = Agv - [(nh - 1)+ 0.5] dh tp x2
 = 4.641
[in2]

Net area subject to tension
when sheared out by 2 side strips
Ant
 = ( ev - 0.5 dh ) tp x 2
 = 0.703
[in2]


Block shear strength required
Vu
 = 
 = 25.00
[kips]

Uniform tension stress factor
Ubs
 = 1.00
AISC 14th  Fig C-J4.2
Bolt shear resistance provided
Rn
 = min (0.6Fu Anv , 0.6Fy Agv ) +
 = 226.69
[kips]
AISC 14th  Eq J4-5
Ubs Fu Ant

Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq J4-5
φ Rn
 = 
 = 170.02
[kips]

ratio
 = 0.15
 > Vu
OK
 
End Plate - Shear in Vz - Block Shear - Center Strip
ratio = 23.84 / 185.10
= 0.13
PASS
Plate Block Shear - Center Strip


Bolt hole diameter
bolt dia db
 = 3⁄4
[in]
bolt hole dia dh
 = 7⁄8
[in]
AISC 14th  B4.3b
Plate thickness
tp
 = 0.375
[in]

Plate strength
Fy
 = 50.0
[ksi]
Fu
 = 65.0
[ksi]

Bolt no in ver & hor dir
nv
 = 3
nh
 = 2

Bolt spacing in ver & hor dir
sv
 = 3.500
[in]
sh
 = 4.000
[in]

Bolt edge dist in ver & hor dir
ev
 = 1.375
[in]
eh
 = 1.375
[in]


Gross area subject to shear
Agv
 = [ (nh - 1) sh + eh ] tp x 2
 = 4.031
[in2]

Net area subject to shear
Anv
 = Agv - [(nh - 1)+ 0.5] dh tp x2
 = 3.047
[in2]

Net area subject to tension
when sheared out by center strip
Ant
 = ( nv - 1) ( sv - dh ) tp
 = 1.969
[in2]


Block shear strength required
Vu
 = 
 = 23.84
[kips]

Uniform tension stress factor
Ubs
 = 1.00
AISC 14th  Fig C-J4.2
Bolt shear resistance provided
Rn
 = min (0.6Fu Anv , 0.6Fy Agv ) +
 = 246.80
[kips]
AISC 14th  Eq J4-5
Ubs Fu Ant

Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq J4-5
φ Rn
 = 
 = 185.10
[kips]

ratio
 = 0.13
 > Vu
OK
 
End Plate - Shear in Vz - Block Shear - 2-Side Strip
ratio = 23.84 / 123.40
= 0.19
PASS
Plate Block Shear - 2 Side Strips


Bolt hole diameter
bolt dia db
 = 3⁄4
[in]
bolt hole dia dh
 = 7⁄8
[in]
AISC 14th  B4.3b
Plate thickness
tp
 = 0.375
[in]

Plate strength
Fy
 = 50.0
[ksi]
Fu
 = 65.0
[ksi]

Bolt no in ver & hor dir
nv
 = 3
nh
 = 2

Bolt spacing in ver & hor dir
sv
 = 3.500
[in]
sh
 = 4.000
[in]

Bolt edge dist in ver & hor dir
ev
 = 1.375
[in]
eh
 = 1.375
[in]


Gross area subject to shear
Agv
 = [ (nh - 1) sh + eh ] tp x 2
 = 4.031
[in2]

Net area subject to shear
Anv
 = Agv - [(nh - 1)+ 0.5] dh tp x2
 = 3.047
[in2]

Net area subject to tension
when sheared out by 2 side strips
Ant
 = ( ev - 0.5 dh ) tp x 2
 = 0.703
[in2]


Block shear strength required
Vu
 = 
 = 23.84
[kips]

Uniform tension stress factor
Ubs
 = 1.00
AISC 14th  Fig C-J4.2
Bolt shear resistance provided
Rn
 = min (0.6Fu Anv , 0.6Fy Agv ) +
 = 164.53
[kips]
AISC 14th  Eq J4-5
Ubs Fu Ant

Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq J4-5
φ Rn
 = 
 = 123.40
[kips]

ratio
 = 0.19
 > Vu
OK
 
 
End Plate / Column Web - Bolt Shear
ratio = 34.54 / 107.35
= 0.32
PASS
Bolt group forces
shear Vy
 = 25.00
[kips]
shear Vz
 = 23.84
[kips]

Shear resultant force
R
 = ( V2y + V2z )0.5
 = 34.54
[kips]


Bolt shear stress
grade
 = A325-N
Fnv
 = 54.0
[ksi]
AISC 14th  Table J3.2
bolt dia db
 = 0.750
[in]
bolt area Ab
 = 0.442
[in2]

Number of bolt carried shear
ns
 = 6.0
shear plane m
 = 1

Bolt group eccentricity coefficient
Cec
 = 
 = 1.000

Required shear strength
Vu
 = 
 = 34.54
[kips]

Bolt shear strength
Rn
 = Fnv Ab ns m Cec
 = 143.14
[kips]
AISC 14th  Eq J3-1
Bolt resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq J3-1
φ Rn
 = 
 = 107.35
[kips]

ratio
 = 0.32
 > Vu
OK
 
 
Bolt Tensile Prying Action on End Plate
ratio = 2.50 / 8.03
= 0.31
PASS
Bolt group forces
shear V
 = 34.54
[kips]
axial P
 = -15.00
[kips]


Single Bolt Tensile Capacity Without Considering Prying
Bolt grade
grade
 = A325-N

Nominal tensile/shear stress
Fnt
 = 90.0
[ksi]
Fnv
 = 54.0
[ksi]
AISC 14th  Table J3.2
bolt dia db
 = 0.750
[in]
bolt area Ab
 = 0.442
[in2]

Bolt group shear force
shear V
 = 34.54
[kips]
no of bolt n
 = 6

Shear stress required
frv
 = V / ( n Ab )
 = 13.03
[ksi]

Resistance factor-LRFD
φ
 = 0.75
AISC 14th  J3.7
Modified nominal tensile stress
F'nt
 = 1.3 Fnt -
Fnt/φ Fnv
frv ≤ Fnt
 = 88.04
[ksi]
AISC 14th  Eq J3-3a
Bolt norminal tensile strength
rn
 = F'nt Ab
 = 38.89
[kips]
AISC 14th  Eq J3-1
Resistance factor-LRFD
φ
 = 0.75
AISC 14th  J3.6
Single bolt tensile capacity
φ rn
 = 
 = 29.17
[kips]


Single Bolt Tensile Capacity After Considering Prying
End plate
width w
 = 6.750
[in]
bolt gage g
 = 4.000
[in]

web tw
 = 0.335
[in]


Dist from bolt center to plate edge
a
 = 0.5 (w - g)
 = 1.375
[in]

a'
 = a + 0.5 db ≤ (1.25 b + 0.5 db )
 = 1.750
[in]
AISC 14th  Eq 9-27

Bolt hole diameter
bolt dia db
 = 0.750
[in]
bolt hole dia dh
 = 0.813
[in]
AISC 14th  B4.3b
Dist from bolt center to face of web
b
 = 0.5(g - tw )
 = 1.833
[in]

b'
 = b - 0.5 db
 = 1.458
[in]
AISC 14th  Eq 9-21

Bolt pitch spacing
sv
 = 3.500

Bolt tributary length
p
 = sv     p ≤ 2b  and p ≤ sv
 = 3.250
[in]
AISC 14th  Page 9-11

ρ
 = b' / a'
 = 0.833
AISC 14th  Eq 9-26
δ
 = 1 - dh / p
 = 0.750
AISC 14th  Eq 9-24
Tensile capacity per bolt before considering prying
B
 = from calc shown in above section
 = 29.17
[kips]

Resistance factor-LRFD
φ
 = 0.90
AISC 14th  Page 9-10
End plate thickness
t
 = 0.375
[in]
tensile Fu
 = 65.0
[ksi]

Plate thickness req'd to develop bolt tensile capacity without prying
tc
 = (
4 B b'/φ p Fu
)0.5
 = 0.946
[in]
AISC 14th  Eq 9-30a
α'
 = 
1/δ (1 + ρ )
[ (
tc/t
)2 - 1 ]
 = 3.900
AISC 14th  Eq 9-35
when  α' > 1
Q
 = (
t/tc
)2 (1 + δ )
 = 0.275
AISC 14th  Eq 9-34
 
Bolt tensile force per bolt in demand
T
 = from calc shown below
 = 2.50
[kips]

 
Tensile strength per bolt after considering prying
φ rn
 = B x Q
 = 8.03
[kips]
AISC 14th  Eq 9-31
ratio
 = 0.31
 > T
OK

Calculate Max Single Bolt Tensile Load
Bolt group force
axial P
 = 15.00
[kips]

 
Bolt number
Bolt Row nh
 = 2
Bolt Col nv
 = 3

Bolt tensile force per bolt
T
 = P / ( nv nh )
 = 2.50
[kips]

 
 
Beam Web Weld Strength
ratio = 4.03 / 9.80
= 0.41
PASS
Weld Group Forces
Web weld shear force
Vu
 = ( V2y + V2z )0.5
 = 34.54
[kips]

Weld group forces
shear V
 = 34.54
[kips]
axial P
 = -15.00
[kips]   in tension
 
Beam web-end plate weld length
L
 = 
 = 9.350
[in]

Beam web-end plate fillet weld size
w
 = 
 = 0.375
[in]

 
Combined Weld Stress
Weld stress from axial force
fa
 = P / L
 = -1.604
[kip/in]
in tension
Weld stress from shear force
fv
 = V / L
 = 3.695
[kip/in]

Weld stress combined - max
fmax
 = ( f2a + f2v )0.5
 = 4.028
[kip/in]
AISC 14th  Eq 8-11
Weld stress load angle
θ
 = tan-1 (
fa/fv
)
 = 23.5
[°]

Fillet Weld Strength Calc
Fillet weld leg size
w
 = 3⁄8
[in]
load angle θ
 = 23.5
[°]

Electrode strength
FEXX
 = 70.0
[ksi]
strength coeff C1
 = 1.00
AISC 14th  Table 8-3
Number of weld line
n
 = 2   for double fillet

Load angle coefficient
C2
 = ( 1 + 0.5 sin1.5 θ )
 = 1.13
AISC 14th  Page 8-9
Fillet weld shear strength
Rn-w
 = 0.6 (C1 x 70 ksi) 0.707 w n C2
 = 25.069
[kip/in]
AISC 14th  Eq 8-1

Base metal - beam web
thickness t
 = 0.335
[in]
tensile Fu
 = 65.0
[ksi]

Base metal - beam web is in shear, shear rupture as per AISC 14th  Eq J4-4 is checked
AISC 14th  J2.4
Base metal shear rupture
Rn-b
 = 0.6 Fu t
 = 13.065
[kip/in]
AISC 14th  Eq J4-4

Double fillet linear shear strength
Rn
 = min ( Rn-w , Rn-b )
 = 13.065
[kip/in]
AISC 14th  Eq 9-2
Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq 8-1
φ Rn
 = 
 = 9.799
[kip/in]

ratio
 = 0.41
 > fmax
OK
 
 
 
Brace Force Load Case 2
shear V = 26.16 kips     axial P = -15.00 kips (T)
ratio = 0.47
PASS
Beam - Shear Yielding - Vy
ratio = 25.00 / 121.61
= 0.21
PASS
Section Shear Yielding Check


Sect yield strength
Fy
 = 50.0
[ksi]

Sect gross area in shear
Agv
 = 
 = 4.054
[in2]

Shear force required
Vu
 = 
 = 25.00
[kips]

Sect shear yielding strength
Rn
 = 0.6 Fy Agv
 = 121.61
[kips]
AISC 14th  Eq J4-3
Resistance factor-LRFD
φ
 = 1.00
AISC 14th  Eq J4-3
φ Rn
 = 
 = 121.61
[kips]

ratio
 = 0.21
 > Vu
OK
 
Beam - Shear Rupture - Vy
ratio = 25.00 / 118.56
= 0.21
PASS
Section Shear Rupture Check


Sect tensile strength
Fu
 = 65.0
[ksi]

Sect net area in shear
Anv
 = 
 = 4.054
[in2]

Shear force in demand
Vu
 = 
 = 25.00
[kips]

Sect shear rupture strength
Rn
 = 0.6 Fu Anv
 = 158.09
[kips]
AISC 14th  Eq J4-4
Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq J4-4
φ Rn
 = 
 = 118.56
[kips]

ratio
 = 0.21
 > Vu
OK
 
Beam - Shear Yielding - Vz
ratio = 26.16 / 277.73
= 0.09
PASS
Section Shear Yielding Check


Sect yield strength
Fy
 = 50.0
[ksi]

Sect gross area in shear
Agv
 = 
 = 9.258
[in2]

Shear force required
Vu
 = 
 = 26.16
[kips]

Sect shear yielding strength
Rn
 = 0.6 Fy Agv
 = 277.73
[kips]
AISC 14th  Eq J4-3
Resistance factor-LRFD
φ
 = 1.00
AISC 14th  Eq J4-3
φ Rn
 = 
 = 277.73
[kips]

ratio
 = 0.09
 > Vu
OK
 
Beam - Shear Rupture - Vz
ratio = 26.16 / 270.78
= 0.10
PASS
Section Shear Rupture Check


Sect tensile strength
Fu
 = 65.0
[ksi]

Sect net area in shear
Anv
 = 
 = 9.258
[in2]

Shear force in demand
Vu
 = 
 = 26.16
[kips]

Sect shear rupture strength
Rn
 = 0.6 Fu Anv
 = 361.04
[kips]
AISC 14th  Eq J4-4
Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq J4-4
φ Rn
 = 
 = 270.78
[kips]

ratio
 = 0.10
 > Vu
OK
 
Beam - Axial Tensile Yield - Px
ratio = 15.00 / 589.50
= 0.03
PASS
Gross area subject to tension
Ag
 = 
 = 13.100
[in2]

Steel yield strength
Fy
 = 
 = 50.0
[ksi]

Tensile force required
Pu
 = 
 = 15.00
[kips]

Tensile yielding strength
Rn
 = Fy Ag
 = 655.00
[kips]
AISC 14th  Eq D2-1
Resistance factor-LRFD
φ
 = 0.90
AISC 14th  D2 (a)
φ Rn
 = 
 = 589.50
[kips]
AISC 14th  Eq D2-1
ratio
 = 0.03
 > Pu
OK
 
Beam Web - Axial Tensile Rupture - Px
ratio = 15.00 / 140.45
= 0.11
PASS
End Plate Direct Connect Length Calc
Beam web-end plate weld length
L
 = 
 = 9.350
[in]

Beam web-end plate fillet weld size
w
 = 
 = 0.375
[in]

Beam web-end plate connect length
Lw
 = L - 2 w
 = 8.600
[in]

Plate Tensile Rupture Check


Plate size
width bp
 = 8.600
[in]
thickness tp
 = 0.335
[in]

Plate tensile strength
Fu
 = 65.0
[ksi]

Plate net area in tension
Ant
 = bp tp
 = 2.881
[in2]

Tensile force in demand
Pu
 = 
 = 15.00
[kips]

Plate tensile rupture strength
Rn
 = Fu Ant
 = 187.27
[kips]
AISC 14th  Eq J4-2
Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq J4-2
φ Rn
 = 
 = 140.45
[kips]
AISC 14th  Eq J4-2
ratio
 = 0.11
 > Pu
OK
 
 
End Plate - Shear Yielding - Vy
ratio = 12.50 / 109.69
= 0.11
PASS
Plate Shear Yielding Check


Plate size
width bp
 = 9.750
[in]
thickness tp
 = 0.375
[in]

Plate yield strength
Fy
 = 50.0
[ksi]

Plate gross area in shear
Agv
 = bp tp
 = 3.656
[in2]

Shear force required
Vu
 = 
 = 12.50
[kips]

Plate shear yielding strength
Rn
 = 0.6 Fy Agv
 = 109.69
[kips]
AISC 14th  Eq J4-3
Resistance factor-LRFD
φ
 = 1.00
AISC 14th  Eq J4-3
φ Rn
 = 
 = 109.69
[kips]

ratio
 = 0.11
 > Vu
OK
 
End Plate - Shear Rupture - Vy
ratio = 12.50 / 78.15
= 0.16
PASS
Plate Shear Rupture Check


Bolt hole diameter
bolt dia db
 = 3⁄4
[in]
bolt hole dia dh
 = 7⁄8
[in]
AISC 14th  B4.3b
Number of bolt
n
 = 3

Plate size
width bp
 = 9.750
[in]
thickness tp
 = 0.375
[in]

Plate tensile strength
Fu
 = 65.0
[ksi]

Plate net area in shear
Anv
 = ( bp - n dh ) tp
 = 2.672
[in2]

Shear force required
Vu
 = 
 = 12.50
[kips]

Plate shear rupture strength
Rn
 = 0.6 Fu Anv
 = 104.20
[kips]
AISC 14th  Eq J4-4
Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq J4-4
φ Rn
 = 
 = 78.15
[kips]

ratio
 = 0.16
 > Vu
OK
 
End Plate - Shear Yielding - Vz
ratio = 13.08 / 75.94
= 0.17
PASS
Plate Shear Yielding Check


Plate size
width bp
 = 6.750
[in]
thickness tp
 = 0.375
[in]

Plate yield strength
Fy
 = 50.0
[ksi]

Plate gross area in shear
Agv
 = bp tp
 = 2.531
[in2]

Shear force required
Vu
 = 
 = 13.08
[kips]

Plate shear yielding strength
Rn
 = 0.6 Fy Agv
 = 75.94
[kips]
AISC 14th  Eq J4-3
Resistance factor-LRFD
φ
 = 1.00
AISC 14th  Eq J4-3
φ Rn
 = 
 = 75.94
[kips]

ratio
 = 0.17
 > Vu
OK
 
End Plate - Shear Rupture - Vz
ratio = 13.08 / 54.84
= 0.24
PASS
Plate Shear Rupture Check


Bolt hole diameter
bolt dia db
 = 3⁄4
[in]
bolt hole dia dh
 = 7⁄8
[in]
AISC 14th  B4.3b
Number of bolt
n
 = 2

Plate size
width bp
 = 6.750
[in]
thickness tp
 = 0.375
[in]

Plate tensile strength
Fu
 = 65.0
[ksi]

Plate net area in shear
Anv
 = ( bp - n dh ) tp
 = 1.875
[in2]

Shear force required
Vu
 = 
 = 13.08
[kips]

Plate shear rupture strength
Rn
 = 0.6 Fu Anv
 = 73.13
[kips]
AISC 14th  Eq J4-4
Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq J4-4
φ Rn
 = 
 = 54.84
[kips]

ratio
 = 0.24
 > Vu
OK
 
 
Coped Beam - Flexural Rupture
ratio = 25.00 / 57.56
= 0.43
PASS
Beam section & cope side
sect
 = W12X45
cope side
 = double cope
Beam top flange cope
depth dc
 = 1.250
[in]
length Lc
 = 3.983
[in]

Beam bottom flange cope
depth dc
 = 1.250
[in]
length Lc
 = 3.983
[in]


Beam section elastic modulus
Snet
 = 
 = 5.146
[in3]

Beam section tensile strength
Fu
 = 
 = 65.0
[ksi]

Distance from face of cope to the point of inflection of beam
e
 = 
 = 4.358
[in]
AISC 14th  Page 9-6

Beam end shear force
Vu
 = 
 = 25.00
[kips]

Beam end shear resistance
Rn
 = Fu Snet / e
 = 76.75
[kips]
AISC 14th  Eq 9-4
Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq 9-4
φ Rn
 = 
 = 57.56
[kips]

ratio
 = 0.43
 > Vu
OK
 
Coped Beam - Local Web Buckling
ratio = 25.00 / 53.13
= 0.47
PASS
Beam section & cope side
sect
 = W12X45
cope side
 = double cope
Beam top flange cope
depth dct
 = 1.250
[in]
length Lct
 = 3.983
[in]

Beam bottom flange cope
depth dcb
 = 1.250
[in]
length Lcb
 = 3.983
[in]


Beam section elastic modulus
Snet
 = 
 = 5.146
[in3]

Distance from face of cope to the point of inflection of beam
e
 = 
 = 4.358
[in]
AISC 14th  Page 9-6

Beam section
depth d
 = 12.100
[in]
web tw
 = 0.335
[in]

Fy
 = 50.0
[ksi]
E
 = 29000
[ksi]

fd
 = 3.5 - 7.5 (dct / d)
 = 2.725
AISC 14th  Eq 9-13
Reduced beam depth
h0
 = d - dct - dcb
 = 9.600
[in]

Plate local buckling stress
Fcr
 = 0.62 π E
t2w/Lct h0
fd
 = 451.8
[ksi]
AISC 14th  Eq 9-12
Fcr
 = Fcr   ≤  Fy
 = 50.0
[ksi]
AISC 14th  Eq 9-12

Beam end shear force
Vu
 = 
 = 25.00
[kips]

Beam end shear resistance
Rn
 = Fcr Snet / e
 = 59.04
[kips]
AISC 14th  Eq 9-6
Resistance factor-LRFD
φ
 = 0.90
AISC 14th  Eq 9-6
φ Rn
 = 
 = 53.13
[kips]

ratio
 = 0.47
 > Vu
OK
 
 
End Plate - Bolt Bearing on End Plate - Vy Vz Combined
ratio = 36.18 / 107.35
= 0.34
PASS
The bolt group is oriented so that the shear Vy is in ver. direction and the shear Vz is in hor. direction
 
Bolt group forces
shear Vy
 = 25.00
[kips]
shear Vz
 = 26.16
[kips]

Bolt group resultant force
R
 = ( V2y + V2z )0.5
 = 36.18
[kips]

Resultant force/hor line load angle
θ
 = tan-1 (Vy / Vz )
 = 43.70
[°]


Bolt hole diameter
bolt dia db
 = 0.750
[in]
bolt hole dia dbh
 = 0.813
[in]
AISC 14th  B4.3b
Bolt hole ver. dimension
dv
 = 
 = 0.813
[in]

Bolt hole hor. dimension
dh
 = 
 = 0.813
[in]

Bolt center to bolt hole edge dist
dc
 = 0.5 dbh
 = 0.406
[in]


Bolt no in ver & hor direction
Bolt Row nv
 = 3
Bolt Col nh
 = 2

Bolt spacing
ver sv
 = 3.500
[in]
hor sh
 = 4.000
[in]

Bolt edge distance
ver ev
 = 1.375
[in]
hor eh
 = 1.375
[in]


Bolt clear dist - bot right corner bolt
LcA
 = min (
ev/sin θ
,
eh/cos θ
) - dc
 = 1.496
[in]

Bolt clear dist - right side edge bolt
LcB
 = min (
sv - 0.5dv/sin θ
,
eh/cos θ
) - dc
 = 1.496
[in]

Bolt clear dist - bot side edge bolt
LcC
 = min (
ev/sin θ
,
sh - 0.5dv/cos θ
) - dc
 = 1.584
[in]

Bolt clear dist - inner edge bolt
LcD
 = min (
sv - 0.5dv/sin θ
,
sh - 0.5dv/cos θ
) - dc
 = 4.072
[in]

Single Bolt Shear Strength

Bolt shear stress
bolt grade
 = A325-N
Fnv
 = 54.0
[ksi]
AISC 14th  Table J3.2
bolt dia db
 = 0.750
[in]
bolt area Ab
 = 0.442
[in2]

Single bolt shear strength
Rn-bolt
 = Fnv Ab
 = 23.86
[kips]
AISC 14th  Eq J3-1

Bolt bearing on plate
thick t
 = 0.375
[in]
tensile Fu
 = 65.0
[ksi]

Bolt bearing strength
Rn-br
 = 3.0 db t Fu
 = 54.84
[kips]
AISC 14th  Eq J3-6b

Type A - Bolt Group Bottom Right Corner Bolt
Number of bolt
nA
 = 1

Bolt tear out strength
Rn-tA
 = 1.5 LcA t Fu
 = 54.69
[kips]
AISC 14th  Eq J3-6b
Bolt bearing strength
RnA
 = min ( Rn-tA , Rn-br , Rn-bolt )
 = 23.86
[kips]


Type B - Bolt Group Right Side Edge Bolt
Number of bolt
nB
 = 2

Bolt tear out strength
Rn-tB
 = 1.5 LcB t Fu
 = 54.69
[kips]
AISC 14th  Eq J3-6b
Bolt bearing strength
RnB
 = min ( Rn-tB , Rn-br , Rn-bolt )
 = 23.86
[kips]


Type C - Bolt Group Bottom Side Edge Bolt
Number of bolt
nC
 = 1

Bolt tear out strength
Rn-tC
 = 1.5 LcC t Fu
 = 57.91
[kips]
AISC 14th  Eq J3-6b
Bolt bearing strength
RnC
 = min ( Rn-tC , Rn-br , Rn-bolt )
 = 23.86
[kips]


Type D - Bolt Group Inner Edge Bolt
Number of bolt
nD
 = 2

Bolt tear out strength
Rn-tD
 = 1.5 LcD t Fu
 = 148.87
[kips]
AISC 14th  Eq J3-6b
Bolt bearing strength
RnD
 = min ( Rn-tD , Rn-br , Rn-bolt )
 = 23.86
[kips]


Bolt bearing strength for all bolts
Rn
 = nA RnA + nB RnB + nC RnC + nD RnD
 = 143.14
[kips]

Bolt resistance factor-LRFD
φ
 = 0.75
AISC 14th  J3-10
φ Rn
 = 
 = 107.35
[kips]

ratio
 = 0.34
 > R
OK
 
End Plate - Bolt Bearing on Column Web - Vy Vz Combined
ratio = 36.18 / 107.35
= 0.34
PASS
The bolt group is oriented so that the shear Vy is in ver. direction and the shear Vz is in hor. direction
 
Bolt group forces
shear Vy
 = 25.00
[kips]
shear Vz
 = 26.16
[kips]

Bolt group resultant force
R
 = ( V2y + V2z )0.5
 = 36.18
[kips]

Resultant force/hor line load angle
θ
 = tan-1 (Vy / Vz )
 = 43.70
[°]


Bolt hole diameter
bolt dia db
 = 0.750
[in]
bolt hole dia dbh
 = 0.813
[in]
AISC 14th  B4.3b
Bolt hole ver. dimension
dv
 = 
 = 0.813
[in]

Bolt hole hor. dimension
dh
 = 
 = 0.813
[in]

Bolt center to bolt hole edge dist
dc
 = 0.5 dbh
 = 0.406
[in]


Bolt no in ver & hor direction
Bolt Row nv
 = 3
Bolt Col nh
 = 2

Bolt spacing
ver sv
 = 3.500
[in]
hor sh
 = 4.000
[in]

Bolt edge distance
ver ev
 = 1.375
[in]
hor eh
 = 1.375
[in]


Bolt clear dist - bot right corner bolt
LcA
 = min (
ev/sin θ
,
eh/cos θ
) - dc
 = 1.496
[in]

Bolt clear dist - right side edge bolt
LcB
 = min (
sv - 0.5dv/sin θ
,
eh/cos θ
) - dc
 = 1.496
[in]

Bolt clear dist - bot side edge bolt
LcC
 = min (
ev/sin θ
,
sh - 0.5dv/cos θ
) - dc
 = 1.584
[in]

Bolt clear dist - inner edge bolt
LcD
 = min (
sv - 0.5dv/sin θ
,
sh - 0.5dv/cos θ
) - dc
 = 4.072
[in]

Single Bolt Shear Strength

Bolt shear stress
bolt grade
 = A325-N
Fnv
 = 54.0
[ksi]
AISC 14th  Table J3.2
bolt dia db
 = 0.750
[in]
bolt area Ab
 = 0.442
[in2]

Single bolt shear strength
Rn-bolt
 = Fnv Ab
 = 23.86
[kips]
AISC 14th  Eq J3-1

Bolt bearing on plate
thick t
 = 0.295
[in]
tensile Fu
 = 65.0
[ksi]

Bolt bearing strength
Rn-br
 = 3.0 db t Fu
 = 43.14
[kips]
AISC 14th  Eq J3-6b

Type A - Bolt Group Bottom Right Corner Bolt
Number of bolt
nA
 = 1

Bolt tear out strength
Rn-tA
 = 1.5 LcA t Fu
 = 43.02
[kips]
AISC 14th  Eq J3-6b
Bolt bearing strength
RnA
 = min ( Rn-tA , Rn-br , Rn-bolt )
 = 23.86
[kips]


Type B - Bolt Group Right Side Edge Bolt
Number of bolt
nB
 = 2

Bolt tear out strength
Rn-tB
 = 1.5 LcB t Fu
 = 43.02
[kips]
AISC 14th  Eq J3-6b
Bolt bearing strength
RnB
 = min ( Rn-tB , Rn-br , Rn-bolt )
 = 23.86
[kips]


Type C - Bolt Group Bottom Side Edge Bolt
Number of bolt
nC
 = 1

Bolt tear out strength
Rn-tC
 = 1.5 LcC t Fu
 = 45.56
[kips]
AISC 14th  Eq J3-6b
Bolt bearing strength
RnC
 = min ( Rn-tC , Rn-br , Rn-bolt )
 = 23.86
[kips]


Type D - Bolt Group Inner Edge Bolt
Number of bolt
nD
 = 2

Bolt tear out strength
Rn-tD
 = 1.5 LcD t Fu
 = 117.11
[kips]
AISC 14th  Eq J3-6b
Bolt bearing strength
RnD
 = min ( Rn-tD , Rn-br , Rn-bolt )
 = 23.86
[kips]


Bolt bearing strength for all bolts
Rn
 = nA RnA + nB RnB + nC RnC + nD RnD
 = 143.14
[kips]

Bolt resistance factor-LRFD
φ
 = 0.75
AISC 14th  J3-10
φ Rn
 = 
 = 107.35
[kips]

ratio
 = 0.34
 > R
OK
 
 
End Plate - Shear in Vy - Block Shear - Center Strip
ratio = 25.00 / 192.87
= 0.13
PASS
Plate Block Shear - Center Strip


Bolt hole diameter
bolt dia db
 = 3⁄4
[in]
bolt hole dia dh
 = 7⁄8
[in]
AISC 14th  B4.3b
Plate thickness
tp
 = 0.375
[in]

Plate strength
Fy
 = 50.0
[ksi]
Fu
 = 65.0
[ksi]

Bolt no in ver & hor dir
nv
 = 2
nh
 = 3

Bolt spacing in ver & hor dir
sv
 = 4.000
[in]
sh
 = 3.500
[in]

Bolt edge dist in ver & hor dir
ev
 = 1.375
[in]
eh
 = 1.375
[in]


Gross area subject to shear
Agv
 = [ (nh - 1) sh + eh ] tp x 2
 = 6.281
[in2]

Net area subject to shear
Anv
 = Agv - [(nh - 1)+ 0.5] dh tp x2
 = 4.641
[in2]

Net area subject to tension
when sheared out by center strip
Ant
 = ( nv - 1) ( sv - dh ) tp
 = 1.172
[in2]


Block shear strength required
Vu
 = 
 = 25.00
[kips]

Uniform tension stress factor
Ubs
 = 1.00
AISC 14th  Fig C-J4.2
Bolt shear resistance provided
Rn
 = min (0.6Fu Anv , 0.6Fy Agv ) +
 = 257.16
[kips]
AISC 14th  Eq J4-5
Ubs Fu Ant

Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq J4-5
φ Rn
 = 
 = 192.87
[kips]

ratio
 = 0.13
 > Vu
OK
 
End Plate - Shear in Vy - Block Shear - 2-Side Strip
ratio = 25.00 / 170.02
= 0.15
PASS
Plate Block Shear - 2 Side Strips


Bolt hole diameter
bolt dia db
 = 3⁄4
[in]
bolt hole dia dh
 = 7⁄8
[in]
AISC 14th  B4.3b
Plate thickness
tp
 = 0.375
[in]

Plate strength
Fy
 = 50.0
[ksi]
Fu
 = 65.0
[ksi]

Bolt no in ver & hor dir
nv
 = 2
nh
 = 3

Bolt spacing in ver & hor dir
sv
 = 4.000
[in]
sh
 = 3.500
[in]

Bolt edge dist in ver & hor dir
ev
 = 1.375
[in]
eh
 = 1.375
[in]


Gross area subject to shear
Agv
 = [ (nh - 1) sh + eh ] tp x 2
 = 6.281
[in2]

Net area subject to shear
Anv
 = Agv - [(nh - 1)+ 0.5] dh tp x2
 = 4.641
[in2]

Net area subject to tension
when sheared out by 2 side strips
Ant
 = ( ev - 0.5 dh ) tp x 2
 = 0.703
[in2]


Block shear strength required
Vu
 = 
 = 25.00
[kips]

Uniform tension stress factor
Ubs
 = 1.00
AISC 14th  Fig C-J4.2
Bolt shear resistance provided
Rn
 = min (0.6Fu Anv , 0.6Fy Agv ) +
 = 226.69
[kips]
AISC 14th  Eq J4-5
Ubs Fu Ant

Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq J4-5
φ Rn
 = 
 = 170.02
[kips]

ratio
 = 0.15
 > Vu
OK
 
End Plate - Shear in Vz - Block Shear - Center Strip
ratio = 26.16 / 185.10
= 0.14
PASS
Plate Block Shear - Center Strip


Bolt hole diameter
bolt dia db
 = 3⁄4
[in]
bolt hole dia dh
 = 7⁄8
[in]
AISC 14th  B4.3b
Plate thickness
tp
 = 0.375
[in]

Plate strength
Fy
 = 50.0
[ksi]
Fu
 = 65.0
[ksi]

Bolt no in ver & hor dir
nv
 = 3
nh
 = 2

Bolt spacing in ver & hor dir
sv
 = 3.500
[in]
sh
 = 4.000
[in]

Bolt edge dist in ver & hor dir
ev
 = 1.375
[in]
eh
 = 1.375
[in]


Gross area subject to shear
Agv
 = [ (nh - 1) sh + eh ] tp x 2
 = 4.031
[in2]

Net area subject to shear
Anv
 = Agv - [(nh - 1)+ 0.5] dh tp x2
 = 3.047
[in2]

Net area subject to tension
when sheared out by center strip
Ant
 = ( nv - 1) ( sv - dh ) tp
 = 1.969
[in2]


Block shear strength required
Vu
 = 
 = 26.16
[kips]

Uniform tension stress factor
Ubs
 = 1.00
AISC 14th  Fig C-J4.2
Bolt shear resistance provided
Rn
 = min (0.6Fu Anv , 0.6Fy Agv ) +
 = 246.80
[kips]
AISC 14th  Eq J4-5
Ubs Fu Ant

Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq J4-5
φ Rn
 = 
 = 185.10
[kips]

ratio
 = 0.14
 > Vu
OK
 
End Plate - Shear in Vz - Block Shear - 2-Side Strip
ratio = 26.16 / 123.40
= 0.21
PASS
Plate Block Shear - 2 Side Strips


Bolt hole diameter
bolt dia db
 = 3⁄4
[in]
bolt hole dia dh
 = 7⁄8
[in]
AISC 14th  B4.3b
Plate thickness
tp
 = 0.375
[in]

Plate strength
Fy
 = 50.0
[ksi]
Fu
 = 65.0
[ksi]

Bolt no in ver & hor dir
nv
 = 3
nh
 = 2

Bolt spacing in ver & hor dir
sv
 = 3.500
[in]
sh
 = 4.000
[in]

Bolt edge dist in ver & hor dir
ev
 = 1.375
[in]
eh
 = 1.375
[in]


Gross area subject to shear
Agv
 = [ (nh - 1) sh + eh ] tp x 2
 = 4.031
[in2]

Net area subject to shear
Anv
 = Agv - [(nh - 1)+ 0.5] dh tp x2
 = 3.047
[in2]

Net area subject to tension
when sheared out by 2 side strips
Ant
 = ( ev - 0.5 dh ) tp x 2
 = 0.703
[in2]


Block shear strength required
Vu
 = 
 = 26.16
[kips]

Uniform tension stress factor
Ubs
 = 1.00
AISC 14th  Fig C-J4.2
Bolt shear resistance provided
Rn
 = min (0.6Fu Anv , 0.6Fy Agv ) +
 = 164.53
[kips]
AISC 14th  Eq J4-5
Ubs Fu Ant

Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq J4-5
φ Rn
 = 
 = 123.40
[kips]

ratio
 = 0.21
 > Vu
OK
 
 
End Plate / Column Web - Bolt Shear
ratio = 36.18 / 107.35
= 0.34
PASS
Bolt group forces
shear Vy
 = 25.00
[kips]
shear Vz
 = 26.16
[kips]

Shear resultant force
R
 = ( V2y + V2z )0.5
 = 36.18
[kips]


Bolt shear stress
grade
 = A325-N
Fnv
 = 54.0
[ksi]
AISC 14th  Table J3.2
bolt dia db
 = 0.750
[in]
bolt area Ab
 = 0.442
[in2]

Number of bolt carried shear
ns
 = 6.0
shear plane m
 = 1

Bolt group eccentricity coefficient
Cec
 = 
 = 1.000

Required shear strength
Vu
 = 
 = 36.18
[kips]

Bolt shear strength
Rn
 = Fnv Ab ns m Cec
 = 143.14
[kips]
AISC 14th  Eq J3-1
Bolt resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq J3-1
φ Rn
 = 
 = 107.35
[kips]

ratio
 = 0.34
 > Vu
OK
 
 
Bolt Tensile Prying Action on End Plate
ratio = 2.50 / 8.03
= 0.31
PASS
Bolt group forces
shear V
 = 36.18
[kips]
axial P
 = -15.00
[kips]


Single Bolt Tensile Capacity Without Considering Prying
Bolt grade
grade
 = A325-N

Nominal tensile/shear stress
Fnt
 = 90.0
[ksi]
Fnv
 = 54.0
[ksi]
AISC 14th  Table J3.2
bolt dia db
 = 0.750
[in]
bolt area Ab
 = 0.442
[in2]

Bolt group shear force
shear V
 = 36.18
[kips]
no of bolt n
 = 6

Shear stress required
frv
 = V / ( n Ab )
 = 13.65
[ksi]

Resistance factor-LRFD
φ
 = 0.75
AISC 14th  J3.7
Modified nominal tensile stress
F'nt
 = 1.3 Fnt -
Fnt/φ Fnv
frv ≤ Fnt
 = 86.66
[ksi]
AISC 14th  Eq J3-3a
Bolt norminal tensile strength
rn
 = F'nt Ab
 = 38.29
[kips]
AISC 14th  Eq J3-1
Resistance factor-LRFD
φ
 = 0.75
AISC 14th  J3.6
Single bolt tensile capacity
φ rn
 = 
 = 28.72
[kips]


Single Bolt Tensile Capacity After Considering Prying
End plate
width w
 = 6.750
[in]
bolt gage g
 = 4.000
[in]

web tw
 = 0.335
[in]


Dist from bolt center to plate edge
a
 = 0.5 (w - g)
 = 1.375
[in]

a'
 = a + 0.5 db ≤ (1.25 b + 0.5 db )
 = 1.750
[in]
AISC 14th  Eq 9-27

Bolt hole diameter
bolt dia db
 = 0.750
[in]
bolt hole dia dh
 = 0.813
[in]
AISC 14th  B4.3b
Dist from bolt center to face of web
b
 = 0.5(g - tw )
 = 1.833
[in]

b'
 = b - 0.5 db
 = 1.458
[in]
AISC 14th  Eq 9-21

Bolt pitch spacing
sv
 = 3.500

Bolt tributary length
p
 = sv     p ≤ 2b  and p ≤ sv
 = 3.250
[in]
AISC 14th  Page 9-11

ρ
 = b' / a'
 = 0.833
AISC 14th  Eq 9-26
δ
 = 1 - dh / p
 = 0.750
AISC 14th  Eq 9-24
Tensile capacity per bolt before considering prying
B
 = from calc shown in above section
 = 28.72
[kips]

Resistance factor-LRFD
φ
 = 0.90
AISC 14th  Page 9-10
End plate thickness
t
 = 0.375
[in]
tensile Fu
 = 65.0
[ksi]

Plate thickness req'd to develop bolt tensile capacity without prying
tc
 = (
4 B b'/φ p Fu
)0.5
 = 0.938
[in]
AISC 14th  Eq 9-30a
α'
 = 
1/δ (1 + ρ )
[ (
tc/t
)2 - 1 ]
 = 3.828
AISC 14th  Eq 9-35
when  α' > 1
Q
 = (
t/tc
)2 (1 + δ )
 = 0.279
AISC 14th  Eq 9-34
 
Bolt tensile force per bolt in demand
T
 = from calc shown below
 = 2.50
[kips]

 
Tensile strength per bolt after considering prying
φ rn
 = B x Q
 = 8.03
[kips]
AISC 14th  Eq 9-31
ratio
 = 0.31
 > T
OK

Calculate Max Single Bolt Tensile Load
Bolt group force
axial P
 = 15.00
[kips]

 
Bolt number
Bolt Row nh
 = 2
Bolt Col nv
 = 3

Bolt tensile force per bolt
T
 = P / ( nv nh )
 = 2.50
[kips]

 
 
Beam Web Weld Strength
ratio = 4.19 / 9.80
= 0.43
PASS
Weld Group Forces
Web weld shear force
Vu
 = ( V2y + V2z )0.5
 = 36.18
[kips]

Weld group forces
shear V
 = 36.18
[kips]
axial P
 = -15.00
[kips]   in tension
 
Beam web-end plate weld length
L
 = 
 = 9.350
[in]

Beam web-end plate fillet weld size
w
 = 
 = 0.375
[in]

 
Combined Weld Stress
Weld stress from axial force
fa
 = P / L
 = -1.604
[kip/in]
in tension
Weld stress from shear force
fv
 = V / L
 = 3.870
[kip/in]

Weld stress combined - max
fmax
 = ( f2a + f2v )0.5
 = 4.189
[kip/in]
AISC 14th  Eq 8-11
Weld stress load angle
θ
 = tan-1 (
fa/fv
)
 = 22.5
[°]

Fillet Weld Strength Calc
Fillet weld leg size
w
 = 3⁄8
[in]
load angle θ
 = 22.5
[°]

Electrode strength
FEXX
 = 70.0
[ksi]
strength coeff C1
 = 1.00
AISC 14th  Table 8-3
Number of weld line
n
 = 2   for double fillet

Load angle coefficient
C2
 = ( 1 + 0.5 sin1.5 θ )
 = 1.12
AISC 14th  Page 8-9
Fillet weld shear strength
Rn-w
 = 0.6 (C1 x 70 ksi) 0.707 w n C2
 = 24.909
[kip/in]
AISC 14th  Eq 8-1

Base metal - beam web
thickness t
 = 0.335
[in]
tensile Fu
 = 65.0
[ksi]

Base metal - beam web is in shear, shear rupture as per AISC 14th  Eq J4-4 is checked
AISC 14th  J2.4
Base metal shear rupture
Rn-b
 = 0.6 Fu t
 = 13.065
[kip/in]
AISC 14th  Eq J4-4

Double fillet linear shear strength
Rn
 = min ( Rn-w , Rn-b )
 = 13.065
[kip/in]
AISC 14th  Eq 9-2
Resistance factor-LRFD
φ
 = 0.75
AISC 14th  Eq 8-1
φ Rn
 = 
 = 9.799
[kip/in]

ratio
 = 0.43
 > fmax
OK